ΕΚΘΕΤΙΚΗ ΣΥΝΑΡΤΗΣΗ:
Πατήστε εδώ για να δείτε σχετικό βίντεο στο youtube
Ασκήσεις:
ΕΜΠΕΔΩΣΗΣ
Τί γίνεται στην περίπτωση που έχουμε
![]()
ΑΝΑΠΤΥΞΗΣ
- Θεωρείστε τη συνάρτηση
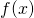
(1) ![]()
Α. Να απαντήσετε αν η συνάρτηση ![]() έχει σημεία τομής με τους άξονες; Αν ναι ποιά είναι αυτά;
έχει σημεία τομής με τους άξονες; Αν ναι ποιά είναι αυτά;
Β. Να βρείτε τις τιμές του α για τις οποίες η συνάρτηση ![]()
- Είναι μια εκθετική συνάρτηση
- Είναι γνησίως αύξουσα στο
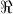
- Είναι γνησίως φθίνουσα στο
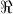
- Έχει σύνολο τιμών
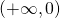
- ικανοποιεί την ανίσωση
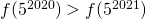
Γ. Μπορείτε να βρείτε τον τυπο της συνάρτησης της οποίας το γράφημα είναι συμμετρικό ως προς τον κατακόρυφο άξονα
2. Να λυθούν οι εξισώσεις:
3. Να λυθούν οι ανισώσεις:
3. Να λυθεί το σύστημα:
![]()
