Η αξία ενός ψηφίου ενός αριθμού εξαρτάται από τη θέση του. Ανάλογα, λοιπόν, τη θέση που βρίσκεται, ένα ψηφίο διαβάζεται διαφορετικά. Αν γνωρίζουμε την αξία αυτήν, θα μπορούμε να κάνουμε πολλά πράγματα: θα μπορούμε να στρογγυλοποιούμε σωστά, θα μπορούμε να διαβάζουμε σωστά έναν δεκαδικό αριθμό και γενικά να συνεννοούμαστε μιλώντας τη γλώσσα των Μαθηματικών.
Ξεκινάμε με ένα παράδειγμα:
Ο αριθμός 213 διαβάζεται διακόσια δεκατρία. Αποτελείται από τρία ψηφία: το 2 (που διαβάζεται 200), το 1 (που διαβάζεται δέκα) και το 3 (που φυσικά διαβάζεται τρία). Και μόνο ακούγοντας τα ψηφία (διακόσια / δέκα / τρία) μπορούμε να καταλάβουμε τι δηλώνουν: το διακόσια δηλώνει εκατοντάδες, το δέκα δηλώνει δεκάδες και το τρία δηλώνει μονάδες. Σωστά;
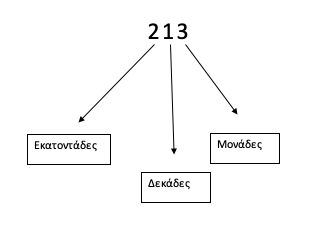
Εύκολος τρόπος για να το θυμόμαστε:
Σε έναν φυσικό αριθμό (1, 2, 3, 4 … 99.987) το τελευταίο ψηφίο στα δεξιά (όπως τον βλέπουμε) δηλώνει μονάδες, το προηγούμενό του -στα αριστερά του- δεκάδες και το προηγούμενο εκατοντάδες. Συνεχίζουμε με μονάδες χιλιάδων, δεκάδες χιλιάδων και εκατοντάδες χιλιάδων / μονάδες εκατομμυρίων, δεκάδες εκατομμυρίων και εκατοντάδες εκατομμυρίων / μονάδες δισεκατομμυρίων … κτλ.
Άλλο παράδειγμα:
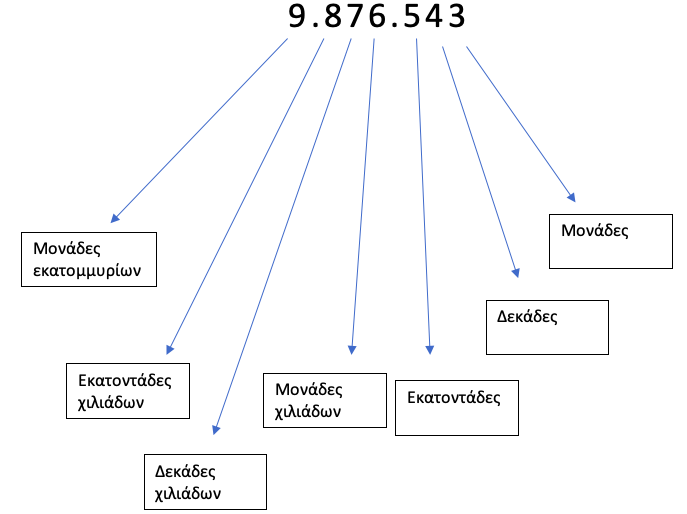
Ο παραπάνω αριθμός διαβάζεται:
- 9 ΕΚΑΤΟΜΜΥΡΙΑ, οκτακόσιες εβδομήντα έξι ΧΙΛΙΑΔΕΣ, πεντακόσια σαράντα τρία.
- Άρα το 9 δηλώνει μονάδες εκατομμυρίων (αφού διαβάζεται 9 εκατομμύρια)
- Το 8 δηλώνει εκατοντάδες χιλιάδων (διαβάζεται οκτακόσια και είναι στις χιλιάδες)
- Το 7 δηλώνει δεκάδες χιλιάδων
- Το 6 δηλώνει μονάδες χιλιάδων
- Το 5 δηλώνει εκατοντάδες (αφού διαβάζεται πεντακόσια)
- Το 4 δηλώνει δεκάδες
- Το 3 δηλώνει μονάδες
Ή αλλιώς: ξεκινάμε από το τέλος και έχουμε: μονάδες / δεκάδες / εκατοντάδες — μονάδες χιλιάδων / δεκάδες χιλιάδων / εκατοντάδες χιλιάδων — μονάδες εκατομμυρίων
Δείτε τώρα έναν δεκαδικό αριθμό:
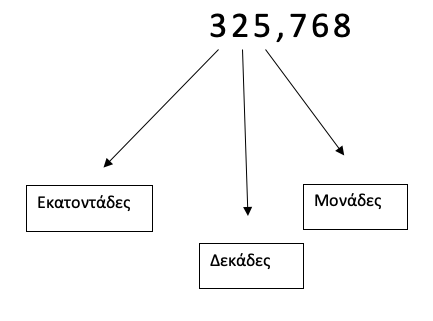
Εδώ ο αριθμός μας έχει ακέραιο μέρος (το 325) και δεκαδικό (το μέρος πίσω από την υποδιαστολή: 768). Για το ακέραιο ισχύει ό,τι είπαμε πριν για τους φυσικούς αριθμούς. Στο δεκαδικό μέρος έχουμε υπο-διαιρέσεις (μικρότερα κομμάτια) της μονάδας (του 1). Έτσι, αν κόψω 1 μέτρο σε 10 ίσα μέρη, θα το έχω μοιράσει σε 10 δέκατα, σε 100 ίσα μέρη, θα το έχω μοιράσει σε 100 εκατοστά, σε χίλια ίσα μέρη, θα το έχω μοιράσει σε 1.000 χιλιοστά. Αυτές είναι και οι βασικές υποδιαιρέσεις που πρέπει να γνωρίζουμε:
- Δέκατα
- Εκατοστά
- Χιλιοστά
Και είναι με αυτή τη σειρά πίσω από την υποδιαστολή! Στο παραπάνω παράδειγμα:
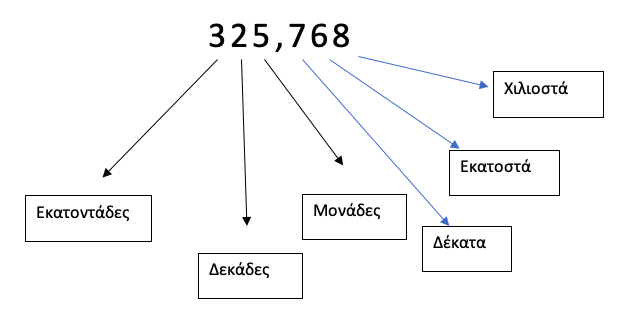
Δείτε τον παραπάνω αριθμό. Τον χωρίσαμε σε ακέραιο και δεκαδικό μέρος. Ξεκινήσαμε από τις Μονάδες (το 5) και προχωρήσαμε στα αριστερά βρίσκοντας τις Δεκάδες (το 2) και τις Εκατοντάδες (το 3). Στη συνέχεια, προχωρήσαμε δεξιά και βρήκαμε τα δέκατα (το 7), τα εκατοστά (το 6) και τα χιλιοστά (το 8).
Αυτό είναι! Τώρα ξέρετε πώς να βρίσκετε την αξία ενός ψηφίου σύμφωνα με τη θέση του.
Και κάτι ακόμα (που συνδέεται με τα παραπάνω):
Διαβάζουμε σωστά έναν δεκαδικό ως εξής:
325,768 –> 325 και 768 χιλιοστά
Δηλαδή:
- Διαβάζουμε το ακέραιο μέρος (325)
- Το , το διαβάζουμε ως «και»
- Διαβάζουμε το δεκαδικό μέρος (768)
- Προσθέτουμε την αξία του τελευταίου ψηφίου του δεκαδικού μέρους (το 8 δηλώνει χιλιοστά)
Κάντε τώρα την παρακάτω άσκηση ως επανάληψη σε όσα διαβάσατε παραπάνω. Αν κάνετε λάθη, ρίξτε άλλη μία ματιά στη θεωρία.
