Ως "εγγραμματισμός" <εγγράμματος + -ισμός, συνών. "εγγραμματοσύνη"> ορίζεται πρωτίστως η ικανότητα ανάγνωσης και γραφής, κυρίως όμως ο επαρκής χειρισμός και η δυναμική αξιοποίηση των αποκτημένων ήδη γνώσεων σε ζητήματα ανάγνωσης και γραφής, προκειμένου να είναι σε θέση κανείς να εφαρμόζει πρακτικά τις γνώσεις αυτές στην καθημερινή του ζωή. Περικλείει, συνεπώς, και την κριτική εγγραμματοσύνη -την ικανότητα, δηλαδή, αφενός της κριτικής στάσης απέναντι σε ποικίλα είδη λόγου και αφετέρου τον ίδιο τον έλεγχο του περιβάλλοντος δια του γραπτού λόγου. Ως "εγγραμματισμό", με άλλα λόγια, ορίζουμε τη δυνατότητα κάποιου να αναγνωρίζει τα σύμβολα του γραπτού λόγου, αλλά, συνάμα, και την ικανότητά του να χρησιμοποιεί με σωστή σειρά τα πεζά και τα κεφαλαία γράμματα, να αντιλαμβάνεται τον τρόπο με τον οποίο εμφανίζονται οι υποσημειώσεις και οι παραπομπές σε ένα κείμενο, τη διαφορά μεταξύ ενός κειμένου επιχειρημάτων και ενός διαφημιστικού φυλλαδίου, το ρόλο των εικόνων σε ένα κείμενο, αλλά και την "ανάγνωση" πινάκων, γραφημάτων και άλλου υποστηρικτικού υλικού που, ενδεχομένως, εντάσσονται σε ένα κειμενικό περιβάλλον.
Εγγραμματισμός στα Μαθηματικά
Η αναζήτηση του εγγραμματισμού στα Μαθηματικά
Στο πλαίσιο του Προγράμματος PISA, ο εγγραμματισμός στα Μαθηματικά ορίζεται ως η ικανότητα του ατόμου να κατανοεί και να εντάσσει την επιστήμη των Μαθηματικών στην καθημερινότητα, να αναπτύσσει τεκμηριωμένες κρίσεις πάνω σε προβλήματα που τίθενται εμπρός του και να χρησιμοποιεί τη μαθηματική γνώση (και τις δεξιότητες που σχετίζονται με αυτή), για να αντιμετωπίζει με επιτυχία τις ανάγκες της καθημερινής ζωής του ως σκεπτόμενος, δημιουργικός και ενεργός πολίτης.
Εκκινώντας από τον ορισμό αυτό, ο εγγραμματισμός στα Μαθηματικά δεν περιορίζεται στη γνώση -απλώς- μαθηματικών όρων, διαδικασιών και μεθόδων που διδάσκονται στο σχολείο. Διότι, παρά το ότι θεωρεί προ-απαιτούμενα όλα τα παραπάνω, ο εγγραμματισμός στα Μαθηματικά αναφέρεται κυρίως στη δυνατότητα δημιουργικής σύνθεσης και εφαρμογής τους, ούτως ώστε, με αφετηρία την ίδια τη μαθηματική γνώση, να είναι εν συνεχεία κανείς σε θέση να αντιμετωπίζει πρακτικά τα πιθανά καθημερινά προβλήματα που ανακύπτουν.
Υπό το πρίσμα αυτό, η έννοια του εγγραμματισμού στα Μαθηματικά συντίθεται από τρία συστατικά στοιχεία, τα οποία αναπαρίστανται στο παρακάτω σχήμα:
Τα συστατικά στοιχεία του εγγραμματισμού στα Μαθηματικά
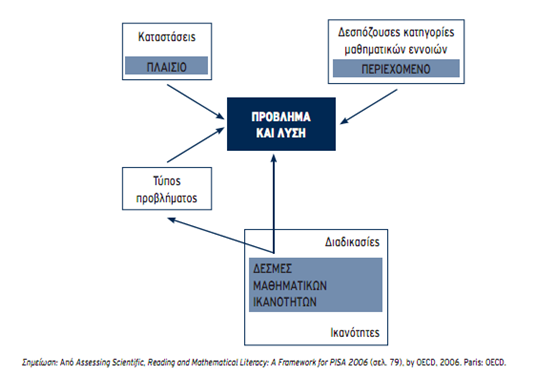
- Το πλαίσιο, στο οποίο εντάσσονται τα προβλήματα, περικλείει προσωπικές, εκπαιδευτικές, επαγγελματικές, κοινωνικές και επιστημονικές καταστάσεις -απλούστερες ή περισσότερο σύνθετες..
- Το μαθηματικό περιεχόμενο προσδιορίζει οτιδήποτε απαιτείται για τη λύση ενός προβλήματος και καθορίζεται από τέσσερις δεσπόζουσες κατηγορίες μαθηματικών εννοιών:
- Χώρος και Σχήμα,
- Μεταβολή και Σχέσεις,
- Ποσότητα,
- Αβεβαιότητα.
- Οι νοητικές διαδικασίες συνδέονται με τις αποκτημένες μαθηματικές ικανότητες και ομαδοποιούνται σε τρεις δέσμες:
- τη δέσμη αναπαραγωγής,
- τη δέσμη συνδέσεων και
- τη δέσμη αναστοχασμού.
