Κριτήρια Διαιρετότητας – Βοήθεια με τις ασκήσεις και τα προβλήματα

Λοιπόν, οι ασκήσεις είναι εύκολες. Στην 1η πρέπει να εφαρμόσουμε τους κανόνες που μάθαμε για τους αριθμούς που διαιρούνται ακριβώς με το 2, το 3 κτλ.

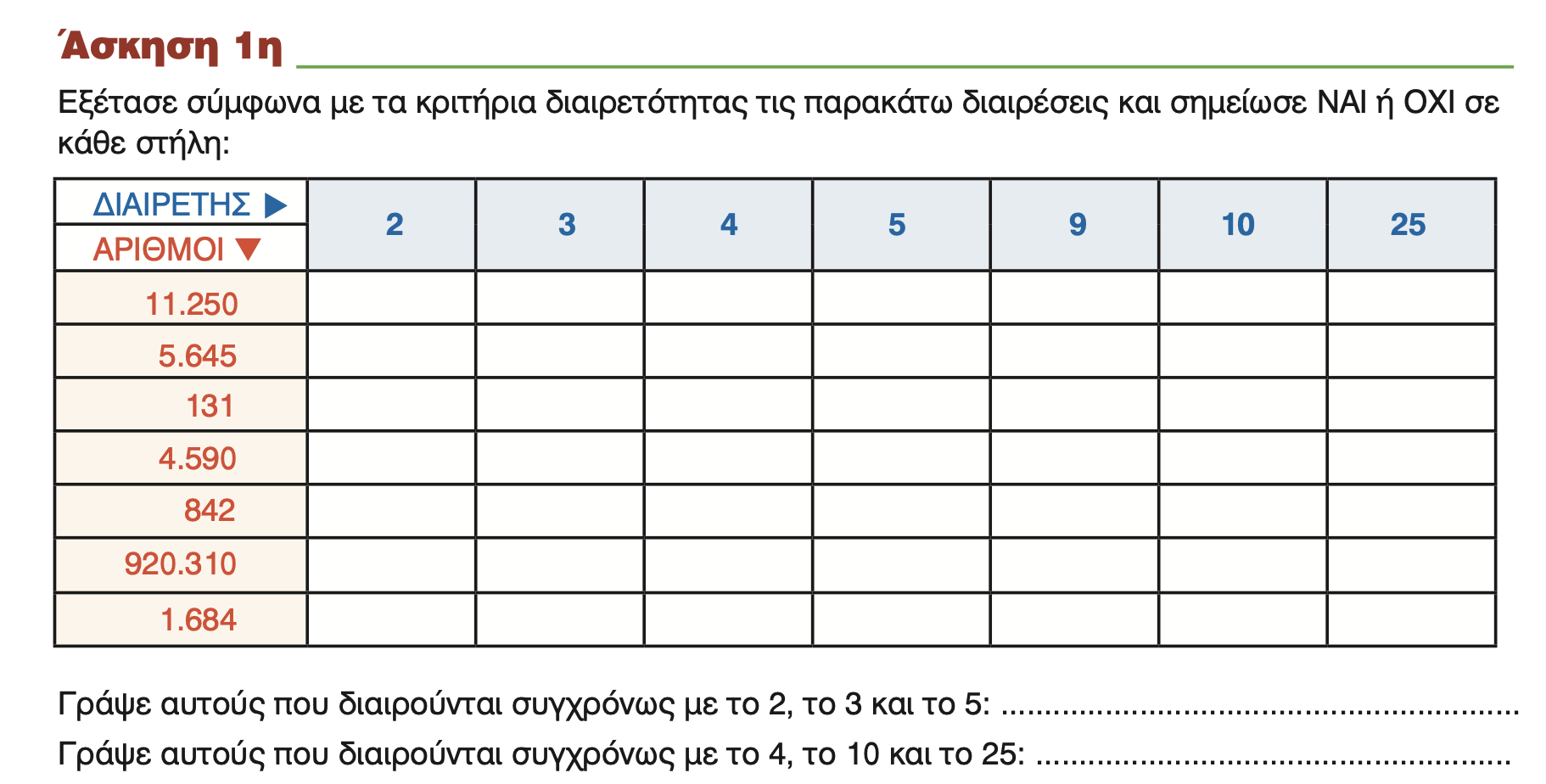
Σκέψη: διαιρείται ακριβώς το 11.250 με το 2; Απάντηση: ναι, επειδή το 11.250 τελειώνει σε 0 (είναι άρτιος αριθμός).

Με το 3; Ναι, επειδή 1 + 1 + 2 + 5 + 0 = 9 (που διαιρείται με το 3). Το ίδιο κάνουμε με όλα τα άλλα.

Η άσκσηση 2 είναι πιο εύκολη από την 1. Πρέπει να γράψετε αριθμούς που διαιρούνται ακριβώς με το 2, το 3 κτλ.

Σας δίνω το 2: 14, 234, 556, 899.850, 4.456 Φρόντισα μόνο οι αριθμοί να είναι άρτιοι.

Θέλουμε αριθμούς που διαιρούνται ταυτόχρονα με το 2, το 4 και το 9. Οπότε πρέπει να χρησιμοποιήσουμε σχεδόν όλα όσα μάθαμε. Ας το κάνουμε με μία σειρά. Πρώτα ας κυκλώσουμε τους αριθμούς που διαιρούνται ακριβώς με το 2.

Στη συνέχεια ψάχνουμε ποιοι από αυτούς διαιρούνται ακριβώς με το 4. Το κόλπο σε αυτή την περίπτωση είναι αν τα τελευταία δύο ψηφία διαιρούνται ακριβώς με το 4 (όταν έχουμε αριθμό που τελειώνει σε 00, τότε διαιρείται, επειδή όλες οι εκατοντάδες διαιρούνται ακριβώς με το 4). Άρα,

• το 100 διαιρείται ακριβώς με το 4
• το 302 (που τελειώνει σε 02) ΔΕ διαιρείται ακριβώς με το 4
• το 150 ΔΕ διαιρείται ακριβώς με το 4

Συνεχίζουμε με τον ίδιο τρόπο και, όταν τελειώσουμε με το 4 προχωράμε στο 9.

Για να λύσουμε το πρόβλημα πρέπει να βρούμε πώς πρέπει να παραταχθούν οι μαθητές ώστε να μην περισσέψει κανένας σε καμία σειρά. Ψάχνουμε δηλαδή να βρούμε πώς θα χωριστούν οι μαθητές σε σειρές. Άρα, ψάχνουμε με ποιους αριθμούς μπορούμε να διαιρέσουμε ακριβώς το 153.

Ξεκινάμε:

• με το 2: Δε διαιρείται ακριβώς, επειδή ο αριθμός είναι μονός (περιττός)
• με το 3? Θα πρέπει να κάνω: 1 + 5 + 3 = 9, που διαιρείται με το 3. Άρα, μπορούν να χωριστούν σε τριάδες.
• με το 4, το 5, το 10; Σίγουρα όχι. Οπότε μένει το 9, για να το κάνετε εσείς.

Εξάσκηση: Παρακάτω μπορείτε να βρείτε το ίδιο πρόβλημα αλλαγμένο λίγο. Μπορείτε να βρείτε τις δύο σωστές απαντήσεις;

Στο πρόβλημα αυτό πρέπει απλώς να αναρωτηθούμε αν χωρά ακριβώς το 3 στο 355. Επίσης, θα είναι καλό να δικαιολογήσουμε την απάντησή μας.

Πριν ξεκινήσουμε μία μικρή συμβουλή: όταν βλέπετε ένα μεγάλο πρόβλημα μην τρομάζετε!

Από όλα όσα λέει το συγκεκριμένο (πολυλογούδικο) πρόβλημα κρατάμε ότι οι αριθμοί μας θα είναι μεταξύ 0 και 39. Όμως, οι πιο σημαντικές πληροφορίες βρίσκονται στις 3 κουκίδες:

Κουκίδα 1: ψάχνουμε έναν μονοψήφιο αριθμό που να διαιρείται ακριβώς με το 2 και το 3!!! Είναι πανεύκολο. Σκέφτομαι: οι μονοψήφιοι που διαιρούνται με το 2 είναι: 2, 4, 6, 8. Από αυτούς διαιρείται με το 3 μόνο το 6!

Κουκίδα 2: Ψάχνουμε ένα διψήφιο που να διαιρείται με το 2, το 3 και το 5. Επειδή το 5 μας αρέσει, ξεκινάμε από το τέλος: 5, 10, 15, 20, 25, 30, 35

Από αυτούς ποιοι διαιρούνται ακριβώς με το 2; Μα φυσικά οι άρτιοι, δηλαδή: 10, 20, 30. Και από αυτούς πρέπει να βρούμε τον ένα που διαιρείται ακριβώς με το 3, ο οποίος φυσικά είναι ___.

Κουκίδα 3: Διψήφιος που να διαιρείται με το 4 και το 9. Συμβουλή: ξεκινήστε με το 9, για να έχετε λιγότερους αριθμούς. Είναι μόνο οι αριθμοί: 18, 27, 36!!!! Από αυτούς θα πρέπει να βρείτε τον ένα που διαιρείται και με το 4! Μόλις τον βρούμε έχουμε λύσει και το πρόβλημα...

Για όσους έφτασαν ως εδώ...

Σας έχει τύχει ποτέ να ψάχνετε τα λόγια ενός τραγουδιού και να μην μπορείτε να το θυμηθείτε ακριβώς; Ε, λοιπόν, αυτό έχει γίνει τραγούδι...