Μαθηματικά – Κλάσματα – Όσα πρέπει να ξέρουμε

Για να είμαστε έτοιμοι για το διαγώνισμα, θα πρέπει να είμαστε σίγουροι ότι μπορούμε να κάνουμε σωστά τα παρακάτω:

1. Να μπορούμε να υπολογίσουμε ισοδύναμα κλάσματα
2. Να μπορούμε να μετατρέψουμε κλάσματα σε δεκαδικούς και δεκαδικούς σε κλάσματα
3. Να μπορούμε να απλοποιήσουμε κλάσματα
4. Να μποροούμε να μετατρέψουμε μεικτούς αριθμούς σε καταχρηστικά κλάσματα και το αντίστροφο
5. Να μπορούμε να μετατρέψουμε ετερώνυμα κλάσματα σε ομώνυμα
6. Να μπορούμε να συγκρίνουμε κλάσματα
7. Να μπορούμε να προσθέσουμε και να αφαιρέσουμε κλάσματα (τα έβαλα μαζί γιατί ακολουθούμε την ίδια διαδικασία)
8. Να μπορούμε να πολλαπλασιάσουμε κλάσματα
9. Να ξέρουμε πώς διαιρούμε κλάσματα
10. Να μπορούμε να λύσουμε αριθμητικές παραστάσεις με κλάσματα
11. Να μπορούμε να λύσουμε προβλήματα με πρόσθεση ή και αφαίρεση κλασμάτων
12. Να μπορούμε να λύσουμε προβλήματα με πολλαπλασιασμό ή διαίρεση κλασμάτων

Πάμε να τα δούμε ένα-ένα:

✅ Ισοδύναμα Κλάσματα

Δύο κλάσματα είναι ισοδύναμα αν εκφράζουν την ίδια ποσότητα.

• Πώς το βρίσκω; Πολλαπλασιάζω ή διαιρώ και τους δύο όρους του κλάσματος (αριθμητή και παρονομαστή) με τον ίδιο αριθμό.

• Παράδειγμα:

   

Τι έκανα; Πολλαπλασίασα αριθμητή και παρονομαστή με τον ίδιο αριθμό (πρώτα το 2 και μετά το 3).

✅ Μετατροπή Κλάσματος σε Δεκαδικό και αντίστροφα

• Κλάσμα σε Δεκαδικό: Διαιρώ τον αριθμητή με τον παρονομαστή.

  •    

    Αν κάνετε τη διαίρεση στο τετράδιό σας θα βρείτε 0,75.

• Δεκαδικός σε Κλάσμα: Γράφω τον αριθμό χωρίς την υποδιαστολή στον αριθμητή. Στον παρονομαστή βάζω το 1 και τόσα μηδενικά όσα ήταν τα δεκαδικά ψηφία.

  •    

✅ Απλοποίηση Κλασμάτων

Κάνουμε το κλάσμα πιο "μικρό" και εύχρηστο.

• Πώς; Διαιρούμε αριθμητή και παρονομαστή με τον Μέγιστο Κοινό Διαιρέτη (Μ.Κ.Δ.) τους. Πώς βρίσκω τον Μ.Κ.Δ.; Δείτε το βίντεο με προσοχή, κάντε δοκιμές (όσες χρειάζεται) στο πρόχειρό σας και θα το μάθετε.

• Παράδειγμα:

     

  Ο Μ.Κ.Δ. (12,16) είναι 4, οπότε διαίρεσα αριθμητή και παρονομαστή με το 4. Αν θέλετε να εξασκηθείτε, απλοποιήστε στο πρόχειρό σας τα κλάσματα 12/15, 20/24, 40/60 μέχρι να γίνουν ανάγωγα (να μην απλοποιούνται άλλο).

 

✅ Μεικτοί αριθμοί & Καταχρηστικά Κλάσματα

• Μεικτός σε Κλάσμα: Πολλαπλασιάζω τον ακέραιο με τον παρονομαστή και προσθέτω τον αριθμητή. Ο παρονομαστής μένει ίδιος.

• Κλάσμα σε Μεικτό: Κάνω τη διαίρεση. Το πηλίκο είναι ο ακέραιος, το υπόλοιπο είναι ο νέος αριθμητής.

✅ Ετερώνυμα κλάσματα σε Ομώνυμα

• Βήμα 1: Βρίσκω το Ε.Κ.Π. των παρονομαστών.

• Βήμα 2: Βάζω "καπελάκια" πάνω από κάθε κλάσμα και βάζω τον αριθμό που αν πολλαπλασιάσω τον παρονομαστή θα γίνει ίσος με το Ε.Κ.Π.

• Προσοχή: Για να κάνουμε τα κλάσματα ομώνυμα, πρέπει να βρούμε το Ε.Κ.Π. Αν απλώς βάλετε τους παρονομαστές χιαστί στα καπελάκια τα καινούργια κλάσματα θα είναι ομώνυμα, αλλά θα είναι ΤΕΡΑΣΤΙΑ!!!  

• Να η διαδικασία (το βήμα 3 εμείς το έχουμε κάνουμε με τα "καπελάκια"):

✅ Σύγκριση Κλασμάτων

Για να συγκρίνω, πρέπει να τα κάνω Ομώνυμα (με τη διαδικασία που βλέπουμε ακριβώς από πάνω). Μετά, μεγαλύτερο είναι αυτό με τον μεγαλύτερο αριθμητή.

---

2. Πράξεις με Κλάσματα

➕➖ Πρόσθεση και Αφαίρεση

ΠΡΟΣΟΧΗ: Μπορώ να προσθέσω ή να αφαιρέσω ΜΟΝΟ Ομώνυμα κλάσματα.

1. Αν είναι ετερώνυμα, τα κάνω πρώτα ομώνυμα (με τη διαδικασία που είδαμε παραπάνω).

2. Προσθέτω ή αφαιρώ τους αριθμητές.

3. Ο παρονομαστής μένει ο ίδιος.

 

✖️ Πολλαπλασιασμός

Εδώ είναι εύκολα τα πράγματα! Δεν χρειάζεται να είναι ομώνυμα.

1. Πολλαπλασιάζω Αριθμητή με Αριθμητή.

2. Πολλαπλασιάζω Παρονομαστή με Παρονομαστή.

 

➗ Διαίρεση

Θυμήσου τον κανόνα: "Αντιστρέφω και Πολλαπλασιάζω".

1. Αφήνω το πρώτο κλάσμα όπως είναι.

2. Μετατρέπω τη διαίρεση σε πολλαπλασιασμό.

3. Αντιστρέφω το δεύτερο κλάσμα.

 

🔢 Αριθμητικές Παραστάσεις

Ακολουθώ τη σωστή σειρά ("προτεραιότητα πράξεων"):

1. Παρενθέσεις

2. Πολλαπλασιασμοί & Διαιρέσεις (από αριστερά προς τα δεξιά)

3. Προσθέσεις & Αφαιρέσεις

Παράδειγμα αριθμητικής παράστασης

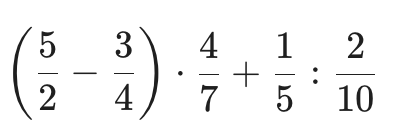
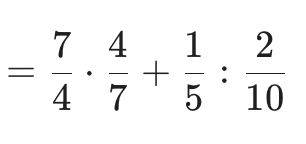
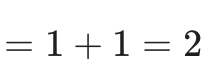
Αν δεν καταλαβαίνετε κάτι, κάντε αναλυτικά τις πράξεις στο τετράδιό σας και θα δείτε ότι θα βρείτε το ίδιο.

 

---

3. Λύνοντας Προβλήματα με κλάσματα

Πώς καταλαβαίνω τι πράξη πρέπει να κάνω;

• Πρόσθεση: Όταν ακούω λέξεις όπως "συνολικά", "όλα μαζί".

• Αφαίρεση: Όταν ψάχνω το "υπόλοιπο", τη "διαφορά", το "πόσο παραπάνω/λιγότερο".

• Πολλαπλασιασμός:

  • Όταν ψάχνω μέρος ενός αριθμού (π.χ., το 1/3​ των 60 ευρώ → 1/3​⋅60/1 = 20 ευρώ).

  • Όταν ξέρω την τιμή της μίας μονάδας (ενός συνόλου) και ψάχνω την τιμή του μέρους.

  • Παράδειγμα: Ο Θοδωρής σκόραρε 36 πόντους σε έναν αγώνα μπάσκετ. Από αυτούς τα 3/4 τους σκόραρε με τρίποντα. Πόσους πόντους σημείωσε με τρίποντα; --> Ξέρω το σύνολο των πόντων του Θοδωρή (τα 4/4) και ψάχνω τα 3/4. Θα κάνω πολλαπλασιασμό: 36 $\cdot$ 3/4 και θα βρω τους πόντους του Θοδωρή.

    Β΄ τρόπος: "Ξαναχτίζω" το πρόβλημα, όπως είδαμε σήμερα στην τάξη
    Τα 4/4 των πόντων του Θοδωρή είναι 36
    Το 1/4 των πόντων του Θοδωρή είναι 36 : 4 = 9 πόντοι
    Τα 3/4 των πόντων του Θοδωρή θα είναι 9 x 3 = 27

    Είναι λογική η απάντηση; Αν όλοι οι πόντοι που σκόραρε ο Θοδωρής είναι 36, τότε τα 3/4 των πόντων του είναι 27.

• Διαίρεση:

  • Όταν μοιράζω κάτι σε ίσα μέρη.

  • Όταν θέλω να δω "πόσες φορές χωράει" το ένα στο άλλο.

  • Όταν ξέρω την τιμή του κλάσματος και ψάχνω τη μονάδα (ή όλο τον πληθυσμό).

  • Παράδειγμα: Τα 3/8 των παικτών του Παναθηναϊκού προέρχονται από την Ευρώπη και είναι 12 ποδοσφαιριστές. Πόσοι είναι οι ποδοσφαιριστές του Παναθηναϊκού; Ξέρω τα 3/8 πόσοι παίκτες είναι και ψάχνω τα 8/8, όλους τους παίκτες. Θα κάνω διαίρεση:
    12 : 3/8Β΄ τρόπος: "Ξαναχτίζω" το πρόβλημα, όπως είδαμε σήμερα στην τάξη
    Τα 3/8 των παικτών είναι 12
    Το 1/8 των παικτών είναι 12 : 3 = 4 παίκτες
    Τα 8/8 των παικτών είναι 4 x 8 = 32 παίκτες

    Είναι λογική η απάντηση; Αν όλοι οι τα 3/8 των παικτών είναι 12, τότε όλοι είναι 32. Μια χαρά λογική είναι η απάντησή μας.

---