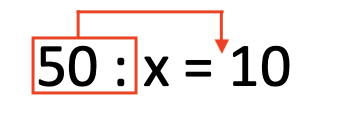Μαθηματικά – Βοήθεια για τις ασκήσεις των Χριστουγέννων

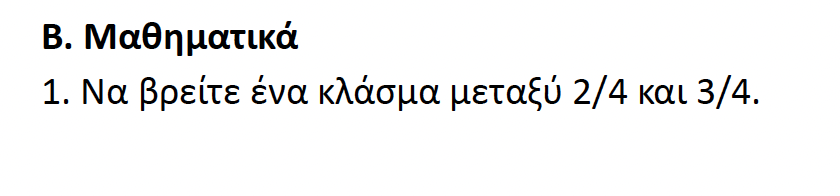
Πρόβλημα 1ο: Πώς θα βρούμε ένα κλάσμα ανάμεσα στα

   

;

Επειδή ανάμεσα στους δύο αριθμητές δεν υπάρχει κανένας αριθμός, θα πρέπει να αλλάξουμε λίγο τα κλάσματα φτιάχνοντας ισοδύναμά τους:

   

Αν πολλαπλασιάσω αριθμητή και παρονομαστή με το 2, τα 2/4 γίνονται 4/8. Το ίδιο κάνω και με τα 3/4. Το κλάσμα που θα σχηματιστεί θα δείτε ότι θα μας δίνει τη δυνατότητα να βρούμε κάποιο που βρίσκεται ανάμεσα.

Για τα υπόλοιπα προβλήματα, βοήθεια θα ανεβάσω αργότερα. Μέχρι τότε... τραγούδι που ταιριάζει με την ημέρα:

Πρέπει να συγκρίνουμε τις ψήφους που πήραν η Μελίνα και η Στέλλα. Όμως, δεν μπορούμε να συγκρίνουμε τα κλάσματα 2/5 και 7/20 επειδή δεν είναι ομώνυμα. Άρα, πρέπει να τα κάνουμε ομώνυμα, υπολογίζοντας το Ε.Κ.Π.

Καταρχήν, θα βρούμε πόσο ζυγίζουν όλα τα χρώματα μαζί! Λέξη-κλειδί: όλα μαζί. Πράξη: πρόσθεση.

Επόμενη λεξη-κλειδί: πόσο χρώμα περίσσεψε. Πράξη: αφαίρεση.

Ό,τι βρούμε από τις προσθέσεις, θα το αφαιρέσουμε από το 10.

Λύνεται με δύο τρόπους (θα σας δείξω και τους δύο):

1. Με αναγωγή στη μονάδα:

• Τα 3/12 είναι 3.600 ευρώ.
• Το 1/12 είναι 3.600 : 3 = 1.200 ευρώ
• Τα 12/12 (όλο το ποσό) είναι 1.200 x 12 =_________

2. Με διαίρεση, επειδή ξέρω τα 3/12 και ψάχνω τα 12/12 (όλο το ποσό)

   

Πάλι μπορούμε με δύο τρόπους. Εδώ θα σας δείξω τον δεύτερο, την απευθείας πράξη:

Ξέρουμε πόσο κοστίζει το 1 κιλό (τα 4/4) και ψάχνουμε τα 3/4. Θα κάνουμε πολλαπλασιασμό.

   

Εξάσκούμαστε στον υπολογισμό του Ε.Κ.Π. και του Μ.Κ.Δ.

Αν δε θυμόμαστε πώς βρίσκουμε το Ε.Κ.Π. βλέπουμε το βίντεο:

Για τον Μ.Κ.Δ. βλέπουμε το παρακάτω βίντεο:

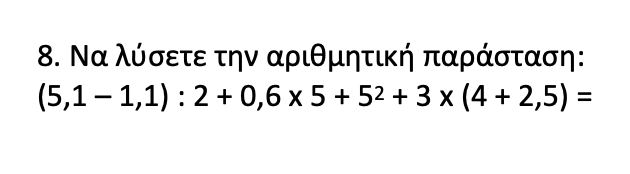
Για να λύσουμε μία αριθμητική παράσταση πρέπει απλά να κάνουμε τις πράξεις με τη σωστή σειρά. Εδώ ξεκινάμε με τις παρενθέσεις, στη συνέχεια κάνουμε τις πράξεις, ξεκινώντας από τη δύναμη.

Η συγκεκριμένη άσκηση αποσκοπεί στο να αυτοματοποιήσουμε κάποιες εύκολες πράξεις και να τις κάνουμε με τον νου. Εδώ θέλω να συνειδητοποιήσουμε ότι:

1 : 2 = 0,5

1 : 4 = 0,25 (το μισό του 0,5)

1 : 8 - 0,125 (το μισό του 0,25)

Σε αυτά τα τρία διαιρώ τον ίδιο αριθμό (το 1) πρώτα με το 2, μετά με το διπλάσιό του, το 4 (με αποτέλεσμα το αποτέλεσμα να είναι το μισό) και μετά με το διπλάσιο του 4, το 8, με αποτέλεσμα το καινούργιο αποτέλεσμα να είναι πάλι το μισό του προηγούμενου.

Το 1 : 3 = 0,33333..... Δεν είναι τέλεια διαίρεση, αλλά βρίσκουμε συνέχεια τριάρια.

Το 2 : 3 = 0,66666... Το διπλάσιο του προηγούμενου.

Το 1 : 5 μπορώ να το βρω από το 10 : 5 κτλ.

Αυτές είναι εξισώσεις που έχουμε κάνει. Επειδή είναι προσθέσεις, για να υπολογίσουμε το x μπορούμε να κάνουμε την αντίστροφη πράξη (αφαίρεση).

2 + x = 34

x = 34 - 2

x = 22

Δείτε τα βήματα. Κάντε το ίδιο με τις υπόλοιπες προσθέσεις.

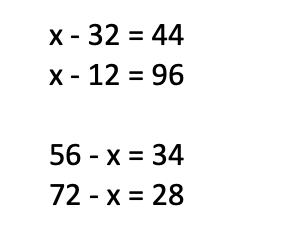
Αφαιρέσεις, πολλαπλασιασμούς και διαιρέσεις δεν έχουμε κάνει. Μπορείτε όμως να προσπαθήσετε να υπολογίσετε το x σκεπτόμενοι λογικά. Στις αφαιρέσεις σημασία έχει ποιος είναι ο άγνωστος: ο πρώτος αριθμός (ο μειωτέος) ή ο δεύτερος (ο αφαιρετέος).

Πρέπει πάντα να θυμόμαστε ότι σε μία αφαίρεση ο μεγαλύτερος αριθμός είναι ο μειωτέος. 

Άρα, για να τον υπολογίσουμε κάνουμε:

x - 32 = 44

x = 44 + 32

x = 76

Αν όμως ο άγνωστος είναι ο αφαιρετέος, κάνουμε το εξής:

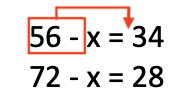
Συγκρατήστε αυτή την εικόνα. Ο πρώτος αριθμός (ο μειωτέος) μεταφέρεται στην άλλη πλευρά μαζί με το - και τον βάζουμε μπροστά από το αποτέλεσμα, τη διαφορά. Αυτό συμβαίνει επειδή σε αυτή την περίπτωση ο μειωτέος είναι ο μεγαλύτερος αριθμός.

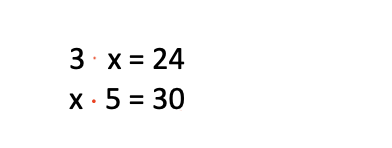
Εδώ είναι πολλαπλασιασμός. Για να βρούμε το x κάνουμε απλώς την αντίστροφη πράξη. Άρα:

3 . x = 24
x = 24 : 3
x = 8

Στη διαίρεση ισχύει ό,τι και στην αφαίρεση: έχει σημασία η θέση του x. Αν είναι μπροστά, κάνουμε την αντίστροφη πράξη (ο διαιρετέος). Αν είναι πίσω (ο διαιρέτης) μεταφέρουμε τον διαιρετέο μαζί με το :

Δείτε τα παραδείγματα:

x : 4 = 8
x = 8 . 4
x = 32

και (όπως και στην αφαίρεση):