Προετοιμασία για διαγώνισμα στα κλάσματα.

Βοήθεια για τα Μαθηματικά

1. Στην άσκηση 1 πρέπει να φτιάξουμε ισοδύναμα κλάσματα. Βλέπουμε, π.χ., ότι το 1/6 = 3/18, επειδή πολλαπλασιάσαμε αριθμητή και παρονομαστή με το 3. Το ίδιο κάνουμε και με τους άλλους δύο αριθμούς.

2. Εδώ τα πράγματα είναι λίγο πιο δύσκολα.
Τα 7/9 είναι εύκολα. Το ίδιο και το επόμενο κλάσμα, τα 2 3/4. Συμπληρώνουμε το 2 και φτιάχνουμε ισοδύναμο κλάσμα με τα 3/4. Φροντίζουμε να πολλαπλασιάζουμε με τον ίδιο αριθμό τον αριθμητή και τον παρονομαστή.

Λίγο πιο δύσκολα εδώ είναι τα 15/20. Σε αυτή την περίπτωση θα βοηθήσει να απλοποιήσουμε πρώτα το κλάσμα (διαιρώντας αριθμητή και παρονομαστή με τον Μ.Κ.Δ. που είναι το 5) και στη συνέχεια να υπολογίσουμε το ισοδύναμο κλάσμα με αριθμητή το 9.

3. Για να φτιάξουμε ανάγωγα κλάσματα, πρέπει να υπολογίσουμε τον Μέγιστο Κοινό Διαιρέτη, τον αριθμό, δηλαδή, που διαιρεί αριθμητή και παρονομαστή. Στη συνέχεια διαιρούμε αριθμητή και παρονομαστή με τον Μ.Κ.Δ. Τα νέα κλάσματα είναι ανάγωγα.

 

 

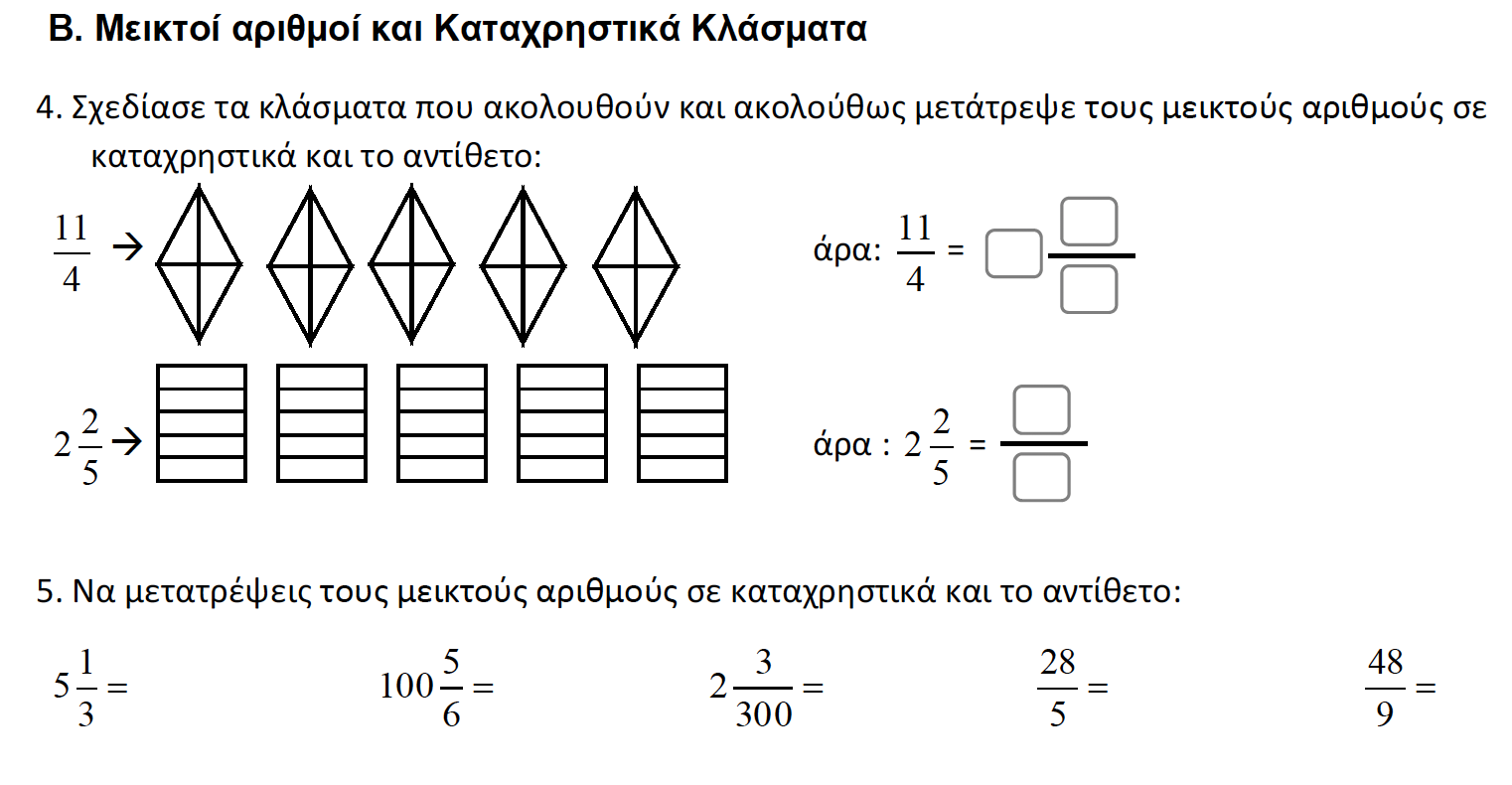
Ακολουθούμε τους τρόπους που ξέρουμε και κάνουμε τις μετατροπές. Ένα παράδειγμα εδώ:

$\displaystyle
\begin{array}{l}
5\frac{1}{3} =\frac{5x3+1}{3} = \frac{16}{3}
\end{array}
$

Υπολογίστε με τον ίδιο τρόπο τα υπόλοιπα.

Δε με νοιάζει τόσο να φαίνεται ο τρόπος σκέψης σας, αλλά θέλω να μπορείτε να δικαιολογήσετε τις απαντήσεις σας. Θυμηθείτε:

α) αν οι αριθμητές είναι ίδιοι, μεγαλύτερο είναι το κλάσμα με τον μικρότερο παρονομαστή (επειδή τα κομμάτια είναι μεγαλύτερα),

β) αν οι παρονομαστές είναι διαφορετικοί, μπορούμε να κάνουμε τα κλάσματα ομώνυμα, ξεκινώντας τη διαδικασία με τα τρία βήματα (πρώτα υπολογίζουμε το Ε.Κ.Π. κτλ.)

Μην ψάχνετε! Κάντε τα ομώνυμα. Ειδικά στα δεύτερα (1/2, 5/6 κτλ.), το Ε.Κ.Π. είναι εύκολο.

Με τον τρόπο που σας έδειξα στο σχολείο:

• Ξέρουμε ότι όλα τα χρήματα (τα 5/5) είναι 240€.
• Ψάχνουμε τα 2/5
• Κάνουμε: Πολλαπλασιασμό 

{Γιατί όταν ξέρουμε το πόσα είναι όλα τα χρήματα και ψάχνουμε ένα μέρος τους κάνουμε πολλαπλασιασμό}

Έτσι θα βρούμε πόσα ξόδεψε τη Δευτέρα.

Με τον ίδιο τρόπο υπολογίζουμε πόσα είναι τα 3/8 των χρημάτων του. Άρα, τι πράξη θα κάνουμε; Τα υπόλοιπα κάντε τα μόνοι σας.

Θα σας δείξω όμως εδώ και έναν τρόπο που θα δούμε αύριο μαζί στο σχολείο. Λοιπόν:

• Τα 5/5 των χρημάτων του είναι 240€
• Το 1/5 των χρημάτων του θα είναι 240 : 5 = 48€ (κάνω διαίρεση, επειδή ξέρω τα πολλά [τα 5/5] και ψάχνω το 1 [το 1/5])
• Τα 2/5 των χρημάτων του θα είναι 48 x 2 = 96€ (κάνω πολλαπλασιασμό, επειδή ξέρω το 1 [το 1/5] και ψάχνω τα πολλά [τα 2/5])

 

Λύση

• Ξέρω ότι τα 3/7 είναι 120 αγόρια
• Ψάχνω τα 7/7.
• Πράξη: Διαίρεση

Με τον αυριανό τρόπο:

• Τα 3/7 είναι 120 αγόρια
• Το 1/7 είναι 120 : 3 = 40 παιδιά
• Τα 7/7 (όλα τα παιδιά) είναι: 40 x 7 =280 παιδιά

 

Εδώ πρέπει καταρχήν να βρούμε τι μέρος του συνόλου είναι τα παιδιά. Διαβάστε παρακάτω με προσοχή και σκεφτείτε μαζί μου:

• Θα πρέπει να βρούμε πόσες είναι μαζί οι γυναίκες και οι άνδρες. Για να το υπολογίσουμε αυτό θα κάνουμε πρόσθεση. Αν κάνουμε σωστά τις πράξεις, θα βρούμε ότι είναι τα 7/10. Άρα, τα παιδιά είναι ... (τι θα κάνω για να το βρω;) Θέλω να το σκεφτείτε μόνοι σας και να μου πείτε αύριο την απάντησή σας.
• Οι γυναίκες είπαμε ότι είναι τα 3/5 των θεατών. Μας λέει το πρόβλημα ότι είναι 90.
• Άρα, τα 3/5 είναι 90. Πώς θα υπολογίσουμε τα 5/5;

Λύνουμε τις αριθμητικές παραστάσεις βήμα-βήμα, με τη σειρά που έχουμε δει ότι κάνουμε τις πράξεις. Ξέρουμε πώς κάνουμε προσθέσεις και αφαιρέσεις. Απλώς, αν έχουμε παρένθεση, κάνουμε πρώτα τις πράξεις μέσα σε αυτήν.

Η λύση είναι:

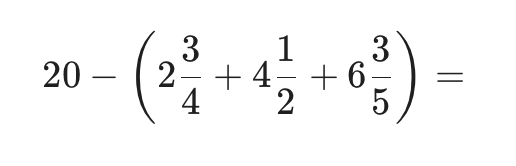
Κάντε μία-μία τις πράξεις και θα το λύσετε.