13 Σεπτεμβρίου 2024

Μαθηματικά – 36 – Μετράω και σχεδιάζω σε κλίμακα (Βοήθεια για τις ασκήσεις)

Εύκολη άσκηση αν καταλάβουμε τι σημαίνει η κλίμακα. Είπαμε ότι είναι ένας αριθμός (πιο σωστά: ένα κλάσμα ή μία διαίρεση) που δείχνει πόσες φορές έχουμε μικρύνει μία απόσταση για να χωρέσει σε έναν χάρτη. Στην περίπτωση α η κλίμακα είναι 1 : 100. Αυτό σημαίνει ότι για να σχεδιάσουμε το τμήμα ΑΒ πρέπει να το μικρύνουμε 100 φορές, κάνοντας διαίρεση:

5 : 100 = 0,05 μ.

Το παραπάνω διαβάζεται: 5 εκατοστά του μέτρου. Στο τετραγωνισμένο χαρτί που βλέπουμε παραπάνω κάθε 1 εκατοστό έχει χωριστεί με πιο έντονα σχεδιασμένες γραμμές. Η γραμμή που θα σχεδιάσουμε θα πρέπει να είναι 5 εκατοστά.

Προβλημα 1

Εδώ μας δίνεται η απόσταση στον χάρτη (18 εκ.) και μας ζητείται η πραγματική απόσταση, που φυσικά είναι μεγαλύτερη. Άρα, για να την υπολογίσουμε θα πρέπει να κάνουμε... πολλαπλασιασμό. Όμως, πριν από αυτό θα πρέπει να κάνουμε τα εκατοστά μέτρα.

18 εκ. = 0,18 μ.

Και...

Τη συνέχεια θα πρέπει να την κάνετε μόνοι σας.

Πρόβλημα 2

Βήμα 1ο

Μετατρέπουμε τα εκατοστά σε μέτρα:

4 εκ. = _____ μ.

Βήμα 2ο

Βρίσκουμε την πραγματική απόσταση κάνοντας:

α. πολλαπλασιασμό

β. διαίρεση

Διαλέξτε πράξη και εκτελέστε την!

Γλώσσα – Διαγώνισμα στην 4η ενότητα – Προετοιμασία

1. Επίθετα σε -ής -ιά -ί και -ύς -ιά -ύ

Μπορούμε να δούμε πώς κλίνονται εδώ:

Εξασκούμαστε

1. Επιλέγουμε τον σωστό τύπο του επιθέτου: https://wordwall.net/resource/82808750
2. Προφορική εξάσκηση: Μπορούμε να κλίνουμε προφορικά τα επίθετα "βυσσινής" και "φαρδύς" στα 3 γένη.

2. Οριστικό και Αόριστο άρθρο

Εξασκούμαστε

1. Παιχνίδι εξάσκησης στη χρήση των οριστικών και αόριστων άρθρων: https://wordwall.net/resource/82809321

3. Αιτιολογικές και χρονικές προτάσεις

Ξεκινούν με αιτιολογικούς και χρονικούς συνδέσμους. Χρησιμοποιούμε τις αιτιολογικές για να δηλώσουμε την αιτία, να αιτιολογήσουμε να δικαιολογήσουμε μία πράξη ή δράση. Χρησιμοποιούμε τις χρονικές για να δηλώσουμε τον χρόνο κατά τον οποίο γίνεται μια πράξη ή δράση. Οι χρονικοί και οι αιτιολογικοί σύνδεσμοι φαίνονται παρακάτω:

Εξασκούμαστε

1. Επανάληψη στις αιτιολογικές προτάσεις: https://wordwall.net/resource/82809817
2. Επανάληψη στις χρονικές προτάσεις: https://wordwall.net/resource/82810056

4. Λεξιλόγιο

Λέξεις που πρέπει να ξέρουμε τι σημαίνουν και πώς γράφονται: κατοικίδιο, καθαρόαιμο, ημίαιμο, υιοθετώ, περιλαίμιο, φιλόζωος, αδέσποτο, κυνοκομείο, κτηνίατρος, κτηνιατρείο

Μαθηματικά – Στρογγυλοποίηση

Θυμάστε πώς κάνουμε στρογγυλοποίηση;

Καταρχήν, ένας αριθμός στρογγυλοποιημένος είναι ένας αριθμός που τελειώνει σε πολλά 0000000. Έχετε σίγουρα ακούσει τους μεγάλους να μιλούν για στρογγυλά ποσά. Αν σας πω ότι ο πληθυσμός της Ελλάδας είναι:

10.413.982

πόσο εύκολα μπορείτε να το θυμάστε; Αν, όμως, σας πω ότι είναι 10.400.000 μάλλον τα πράγματα γίνονται πιο εύκολα.

Τι κάναμε στον παραπάνω αριθμό;

Ήταν 10.413.982. Τον στρογγυλοποιήσαμε στις εκατοντάδες χιλιάδων. Είδαμε τα επόμενα ψηφία και καταλάβαμε ότι είναι πιο κοντά στα 10.400.000 απ' ό,τι στα 10.500.000. Οπότε ο νέος αριθμός έχει περισσότερα μηδενικά στο τέλος κι εγώ μπορώ να τον θυμάμαι πιο εύκολα.

Αν όμως ο αριθμός ήταν 10.475.985 και ήθελα να τον στρογγυλοποιήσω στις εκατοντάδες χιλιάδων τι θα έκανα; Σχεδόν το ίδιο:

Θα σκεφτόμουν ότι ο αριθμός είναι ανάμεσα στα 10.400.000 και τα 10.500.000. Εδώ είναι πιο κοντά στα 10.500.000, οπότε θα τον στρογγυλοποιούσα στα 10.500.000.

Σύμφωνα με το βιβλίο, για να στρογγυλοποιήσουμε έναν αριθμό κάνουμε τα εξής βήματα:

Πιο απλά, τα βήματα αυτά είναι:

• Βρίσκουμε το ψηφίο στο οποίο θέλουμε να στρογγυλοποιήσουμε (δεκάδες, εκατοντάδες, μονάδες χιλιάδων, δεκάδες χιλιάδων κτλ.).

Π.χ., αν θέλουμε να στρογγυλοποιήσουμε τον αριθμό 578.873 στις δεκάδες χιλιάδες, ο αριθμός στις δεκάδες χιλιάδες είναι 7.

• Γράφουμε όλα τα προηγούμενα ψηφία ίδια.

5.......

• Κοιτάμε το επόμενο ψηφίο. Αν είναι 5-9 ετοιμαζόμαστε να αυξήσουμε τον αριθμό μας. Αν είναι 0-4, θα τον αφήσουμε ίδιο. Στον αριθμό μας το επόμενο ψηφίο είναι 8.
• Αλλάζουμε ή αφήνουμε ίδιο το ψηφίο στο οποίο κάνουμε τη στρογγυλοποίηση. Άρα, αφού ο επόμενος αριθμός είναι 8, αυξάνουμε το 7 και κάνουμε όλα τα ψηφία 0. Ο αριθμός στο παράδειγμά μας θα γίνει:

580.000

Μεγαλώσαμε τον αριθμό μας επειδή μετά είχε 8 και κάναμε όλα τα υπόλοιπα ψηφία 0.

Τελικά η στρογγυλοποίηση δεν είναι τόσο δύσκολη!

Επανάληψη 1ης ενότητας – Βοήθεια στις ασκήσεις

Άσκηση 1

Πώς γράφονται τα 200 τρισεκατομμύρια 88; Καταρχήν, τα τρισεκατομμύρια είναι η αμέσως μεγαλύτερη μονάδα σε αξία από τα δισεκατομμύρια. Έτσι, έχουμε: χιλιάδες, εκατομμύρια, δισεκατομμύρια, τρισεκατομμύρια. Άρα, γράφουμε 200. --> η τελεία διαβάζεται "τρισεκατομμύρια". Συνεχίζουμε:

200.000.000.000.088

επειδή έχουμε: 200 τρισεκατομμύρια, 0 δισεκατομμύρια, 0 εκατομμύρια, 0 χιλιάδες και 88 μονάδες.

Άσκηση 3

Εδώ προσέχουμε το εξής: Πρέπει, καταρχήν, να βρούμε τον προηγούμενο και τον επόμενο αριθμό. Στη συνέχεια ελέγχουμε αν είναι άρτιος (ζυγός) ή περιττός (μονός). Αν δεν είναι πηγαίνουμε στο προηγούμενο ή στον επόμενο κτλ. Παράδειγμα:

4.500.000 --> ο προηγούμενός του είναι 4.499.999, ο οποίος είναι περιττός, επειδή τελειώνει σε 9. Όμως, εμείς θέλουμε τον προηγούμενο άρτιο, οπότε πηγαίνουμε στον αμέσως προηγούμενο: 4.499.998, ο οποίος τελειώνει σε 8, οπότε είναι άρτιος. Το ίδιο με τον επόμενο άρτιο, ο οποίος είναι ο: 4.500.002.

Τα προβλήματα δε θα πρέπει να μας δυσκολέψουν.

Το 6 λύνεται βήμα-βήμα, αφού υπολογίσουμε πόσους κουραμπιέδες πουλιούνται κάθε χρόνο.

Το 7 μοιάζει με το 6 στη σελίδα 22 του Τετραδίου Εργασιών: πρέπει να βρούμε σε πόσες ομάδες χωρίζονται οι μαθητές και μετά να υπολογίσουμε τη θέση της Κατερίνας.

Στο 8 πρέπει πρώτα να υπολογίσουμε πόσα βιβλία είχε κάθε σακούλα και μετά να υπολογίσουμε πόσα βιβλία έχουν οι 230 σακούλες.

Οι εγκλίσεις του ρήματος

Διαβάζουμε τη θεωρία όσες φορές χρειάζεται, για να την κατανοήσουμε και στη συνέχεια λύνουμε τις ασκήσεις. Για να ανοίξουν οι ασκήσεις, κάνουμε κλικ πάνω στην εικόνα με τη θεωρία.

Επανάληψη στην Ιστορία – 1η ενότητα – Οι Έλληνες και οι Ρωμαίοι

Ερωτήσεις

• Πότε κατέκτησαν οι Ρωμαίοι τους Έλληνες;
• Ποιο σύστημα εφάρμοσαν οι Ρωμαίοι στη διακυβέρνηση των Ελλήνων; Τι σημαίνει η φράση αυτή;

Απαντήσεις

Οι Ρωμαίοι κατέκτησαν την Ελλάδα το 146 π.Χ. Πρώτη τους φροντίδα ήταν να τους κρατήσουν διχασμένους. Η πολιτική που εφάρμοσαν ονομάστηκε "διαίρει και βασίλευε" (που σημαίνει "χώρισέ τους και κυβέρνησέ τους").

Ερωτήσεις

• Πώς συμπεριφέρθηκαν οι Ρωμαίοι: α) σε αυτούς που δεν τους αντιστάθηκαν;  β) σε αυτούς που τους αντιστάθηκαν;

Απαντήσεις

Στη διοίκηση των ελληνικών πόλεων εφάρμοσαν δύο πολιτικές ανάλογα με τη στάση που αυτές είχαν τηρήσει στους ελληνορωμαϊκούς πολέμους:

1. Σε αυτούς που αντιστάθηκαν φέρθηκαν ανελέητα (γκρέμισαν τα τείχη των πόλεων, άρπαξαν θησαυρούς και έργα τέχνης, επέβαλαν βαρύτατους φόρους, αιχμαλώτισαν τους κατοίκους τους)
2. Σε αυτούς που συμμάχησαν μαζί τους ή δεν αντιστάθηκαν παραχωρούσαν αυτονομία ή ανεξαρτησία και ανέθεταν τη διοίκησή τους σε φιλορωμαίους Έλληνες.

Η παρουσία των Ρωμαίων στις ελληνικές πόλεις είχε δυσάρεστες συνέπειες για τους Έλληνες.

Ερώτηση

• Να αναφέρετε παραδείγματα που δείχνουν ότι οι Ρωμαίοι επηρεάστηκαν από τον πολιτισμό των Ελλήνων. 

Απάντηση

Όταν κατέκτησαν την Ελλάδα οι Ρωμαίοι γνώρισαν και θαύμασαν τον πολιτισμό των Ελλήνων. Τα χρόνια που ακολούθησαν:

• έχτιζαν τα σπίτια τους με ελληνικά σχέδια και τα στόλιζαν με αγάλματα και έργα τέχνης που έκαναν Έλληνες τεχνίτες

Στην εικόνα βλέπουμε το Ηρώδειο, θέατρο κάτω από τον Παρθενώνα. Το θέατρο είναι φτιαγμένο όπως τα αρχαία ελληνικά θέατρα, ενώ και η αρχιτεκτονική του μοιάζει με αυτή των αρχαιοελληνικών κτιρίων και ναών.

• μάθαιναν την ελληνική γλώσσα
• έπαιρναν Έλληνες δασκάλους για τα παιδιά τους και τα έστελναν στην Ελλάδα για να σπουδάσουν
• μετέφραζαν στη λατινική γλώσσα έργα αρχαίων Ελλήνων συγγραφέων
• Ρωμαίοι άρχοντες και αυτοκράτορες δαπανούσαν χρήματα και κοσμούσαν τις ελληνικές πόλεις με σπουδαία έργα

Ερώτηση

• Πώς ονομάστηκε ο πολιτισμός που γεννήθηκε από τη “συνάντηση” Ρωμαίων και Ελλήνων;

Απάντηση

Έτσι, οι δύο αυτοί πολιτισμοί ήρθαν πιο κοντά. Ο πολιτισμός που "γεννήθηκε" ονομάζεται ελληνορωμαϊκός.

Στην εικόνα βλέπουμε το ρωμαϊκό Πάνθεο. Ήταν ένα κτίριο το οποίο ήταν αφιερωμένο στους θεούς των Ρωμαίων και περιελάμβανε και τους θεούς των Ελλήνων. Και σε αυτό φαίνεται η επίδραση των Ελλήνων στον πολιτισμό των Ρωμαίων.

Ερωτήσεις

• Πώς ονόμασαν οι Ρωμαίοι τη Μεσόγειο;
• Ποιος ήταν ο πληθυσμός της αυτοκρατορίας τον 1ο αιώνα μ.Χ.;
• Να αναφέρετε τα μέτρα με τα οποία προσπάθησαν οι Ρωμαίοι να διοικήσουν την απέραντη αυτοκρατορία τους.

Απαντήσεις

Το 100 μ.Χ. οι Ρωμαίοι είχαν κατακτήσει όλες τις χώρες γύρω από τη Μεσόγειο θάλασσα, την οποία ονόμαζαν "η θάλασσά μας" (mare nostrum). Στους Ρωμαίους άρεσε να περηφανεύονται ότι η Μεσόγειος ήταν "ρωμαϊκή λίμνη". Τότε ο πληθυσμός της αυτοκρατορίας ξεπερνούσε τα 50 εκατομμύρια. Οι Ρωμαίοι έγιναν κοσμοκράτορες.

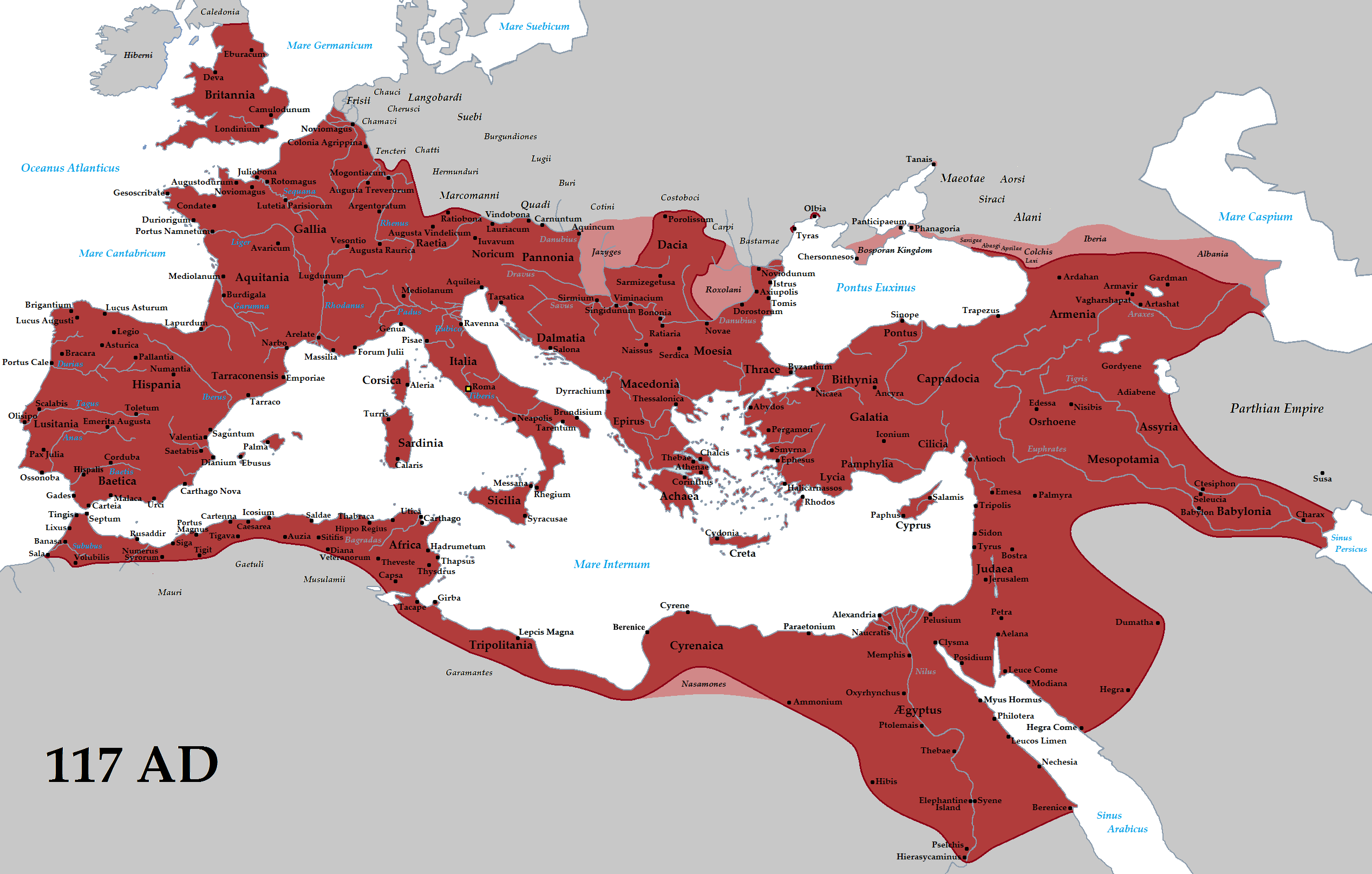
Στην εικόνα βλέπουμε τα σύνορα της ρωμαϊκής αυτοκρατορίας το 117 μ.Χ. Όπως βλέπουμε οι Ρωμαίοι είχαν κατακτήσει όλες τις περιοχές γύρω από τη Μεσόγειο, την οποία αποκαλούσαν mare nostrum ("η δική μας θάλασσα")

Όμως, η αυτοκρατορία ήταν απέραντη και η διοίκησή της δύσκολη. Για να μπορέσουν να τη διοικήσουν οι Ρωμαίοι:

1. όρισαν τον αυτοκράτορα "πρώτο πολίτη" και όλοι όφειλαν υπακοή σε αυτόν
2. έδωσαν τον τίτλο του Ρωμαίου πολίτη σε όσους κατακτημένους αποδέχονταν την κυριαρχία της Ρώμης
3. διόρισαν ανώτερους Ρωμαίους κυβερνήτες (τους ανθύπατους), οι οποίοι επέβλεπαν τους τοπικούς άρχοντες
4. μείωσαν τους φόρους και οργάνωσαν καλύτερα τον τρόπο είσπραξής τους
5. ψήφισαν δικαιότερους νόμους και φρόντιζαν για την τήρησή τους

Ερώτηση

• Πώς ονομάστηκε η περίοδος της κυριαρχίας της Ρώμης σε όλον τον γνωστό τότε κόσμο;

Απάντηση

Την περίοδο εκείνη η Ρώμη αναπτύσσεται, ακμάζει. Η περίοδος αυτή ονομάζεται περίοδος της "ρωμαϊκής ειρήνης" (pax romana).

Η κατασκευή ενός ρωμαϊκού υδραγωγείου την περίοδο της pax romana (ρωμαϊκής ειρήνης). Με τα υδραγωγεία όλες οι μεγάλες πόλεις αποκτούν νερό αρκετό για τις ανάγκες τους.

Ερωτήσεις

• Ποιος ήταν ο πληθυσμός της Ρώμης τον 1ο μ.Χ. αιώνα;
• Πού ζούσαν οι περισσότεροι κάτοικοι της Ρώμης τότε και πού ζούσαν οι πιο εύποροι κάτοικοί της;

Απαντήσεις

Η Ρώμη ήταν χτισμένη πλάι στον ποταμό Τίβερη. Την περίοδο της ακμής της (τον 1ο αιώνα μ.Χ.) ο πληθυσμός της πλησίαζε το ενάμισι εκατομμύριο. Οι περισσότεροι κάτοικοι κατοικούσαν σε πολυκατοικίες και οι πιο εύποροι σε μονοκατοικίες. Το παλάτι των αυτοκρατόρων ήταν στον Παλατίνο λόφο.

Βίντεο: Ψηφιακή αναπαράσταση της αρχαίας Ρώμης

Ερωτήσεις

• Πώς ζούσαν οι μεγαλοϊδιοκτήτες γης στη ρωμαϊκή ύπαιθρο; 
• Πώς ζούσαν οι μικροϊδιοκτήτες γεωργοί στη ρωμαϊκή ύπαιθρο; 
• Πώς διασκέδαζαν οι αρχαίοι Ρωμαίοι;

Απαντήσεις

Οι κάτοικοι της ρωμαϊκής υπαίθρου ήταν γεωργοί, βοσκοί, τεχνίτες και μικροέμποροι. Οι μεγαλοϊδιοκτήτες γης είχαν μεγάλα αγροκτήματα, μέσα στα οποία είχαν τα σπίτια τους, αποθήκες, ορνιθώνες, στάβλους. Όλα αυτά τα φρόντιζαν δούλοι. Οι μικροϊδιοκτήτες καλλιεργούσαν μόνοι τα κτήματά τους και ζούσαν από τα προϊόντα της παραγωγής τους. Τα παιδιά τους συχνά εγκατέλειπαν την ύπαιθρο και αναζητούσαν εργασία στις πόλεις, τις τέχνες, τα δημόσια έργα και τον στρατό.

Όλοι αυτοί πλούσιοι και φτωχοί πήγαιναν συχνά στη Ρώμη και συμμετείχαν σε γιορτές και αγώνες που γίνονταν εκεί.

Βοήθεια στο πρόβλημα 6, Τετράδιο Εργασιών, σελ. 22

Σκεφτόμαστε πώς θα υπολογίσουμε τους ανθρώπους που είναι μπροστά και πίσω από τον κύριο Γιάννη: μπροστά του είναι 5πλάσια από όσα είναι πίσω του.

Άρα θα πρέπει πρώτα να μοιράσουμε τον κόσμο σε 6 μέρη και στη συνέχεια να υπολογίσουμε έτσι τα άτομα, ώστε ο αριθμός που θα βρούμε για τα άτομα που είναι μπροστά να είναι πενταπλάσιος από αυτόν για τα άτομα που είναι πίσω.

Μαθηματικά – Ποσοστά

Πρέπει να καταλάβουμε το εξής: Χρησιμοποιούμε τα ποσοστά για να δείξουμε το μέρος μίας ποσότητας. Αν στις εκλογές δούμε ότι το κόμμα Α πήρε 42% και έχουν ψηφίσει 10.000.000 άνθρωποι, αυτό σημαίνει ότι σε κάθε 100 ανθρώπους οι 42 ψήφισαν το κόμμα Α.

Αν θέλω να υπολογίσω πόσοι άνθρωποι είναι αυτοί, θα κάνω:

Άρα, το 42% αντιστοιχεί στη συγκεκριμένη περίπτωση σε 4.200.000 ανθρώπους. Σε όλα τα προβλήματα με ποσοστά, με κάποιον τρόπο καλούμαστε να βρούμε τον αριθμό στον οποίο αντιστοιχεί το ποσοστό που μας δίνεται. Αυτό γίνεται με τον πολλαπλασιασμό που είδαμε παραπάνω.

Βέβαια, αν έχετε δει τα ποσοστά τη βραδιά των εκλογών ή στις δημοσκοπήσεις θα καταλάβετε αμέσως ότι είναι πιο εύκολο να συγκρίνουμε την επίδοση διαφορετικών κομμάτων με ποσοστά παρά με αριθμούς (προτιμάμε σίγουρα να ξέρουμε ότι το κόμμα Α πήρε 42% και το Β 34%, παρά ότι το Α πήρε 4.284.901 ψήφους και το Β 3.398.875 ψήφους!). Έτσι με τα ποσοστά μπορούμε να κάνουμε εύκολα και γρήγορα συγκρίσεις.

Ας δούμε τώρα την άσκηση 3 από το Τετ. Εργασιών (σελ. 19):

Πώς θα υπολογίσω το 10% των 200€; Μα φυσικά με πολλαπλασιασμό: . Αν θέλετε, μπορείτε να κάνετε την πράξη βήμα-βήμα στο τετράδιό σας και θα δείτε πώς βρήκα το 20!

Για τα άλλα ερωτήματα θα πρέπει να σκεφτώ:
α) το ένα κιλό είναι 1.000 γραμμάρια
β) Η μισή ώρα είναι 30 λεπτά
γ) Τα παιδιά του σχολείου είναι 250.

Σιγά-σιγά θα μάθουμε να κάνουμε γρήγορα και εύκολα πράξεις με ποσοστά!

Ας πούμε: Θα παρατηρήσουμε ότι το 10% ενός αριθμού είναι το 1/10, δηλαδή, μπορώ να το βρω διαιρώντας τον αριθμό με το 10. 

Το 20% ενός αριθμού είναι το 1/5 (όπως το 20 είναι το 1/5 του 100), δηλαδή, μπορώ να το βρω διαιρώντας τον αριθμό με το 5.

Το 25% ενός αριθμού είναι το 1/4, δηλαδή, μπορώ να το υπολογίσω διαιρώντας τον αριθμό με το 4. 

Το 50% ενός αριθμού είναι το 1/2, δηλαδή, μπορώ να το υπολογίσω διαιρώντας τον αριθμό με το 2. 

Άρα, όταν έχω ποσοστά, θα πρέπει να σκεφτώ με λίγη φαντασία και αρκετά δημιουργικά, για να βρω τον αριθμό που ψάχνω.

Για δείτε το παρακάτω πρόβλημα:

30€ κάνει η φόρμα και η έκπτωση είναι 25%. Πόσα ευρώ είναι η έκπτωση; Τι πράξη θα κάνω για να το βρω;

Μα φυσικά πολλαπλασιασμό! Τι θα πολλαπλασιάσω όμως;