Ένα αγώγιμο κυκλικό πλαίσιο με αντίσταση R=0,5Β βρίσκεται μέσα σε ένα μαγνητικό πεδίο με το επίπεδό του κάθετο στις δυναμικές γραμμές, όπως στο πρώτο από τα παρακάτω σχήματα.
October 2021 archive
Oct 14
Η μετακίνηση μιας φορτισμένης σφαίρας. Φ.Ε.
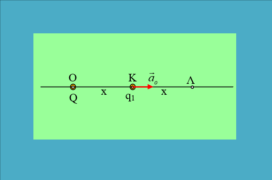
Στο σημείο Ο μιας ευθείας (ε) έχουμε ακλόνητα τοποθετήσει ένα σημειακό θετικό φορτίο Q. Σε μια στιγμή αφήνουμε στο σημείο Κ της ευθείας σε απόσταση (ΟΚ)=x μια μικρή σφαίρα Α μάζας m1= m και φορτίου q1, η οποία αποκτά επιτάχυνση α0, όπως στο σχήμα. Μετά από λίγο η σφαίρα Α περνά από το σημείο Λ, …



Recent Comments