Λίστα άρθρων του συγγραφέα
Ιούλ 25
αα
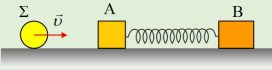
Σε λείο οριζόντιο επίπεδο ηρεμούν δυο σώματα Α και Β, με μάζες m1=1kg και m2=2kg, εμένα στα άκρα ιδανικού ελατηρίου σταθεράς k=24Ν/m.
Ιούλ 20
Δύο χρονοκυκλώματα μαζί!
Για το διπλανό κύκλωμα δίνονται Ε=20V, C=5μF, ενώ ο διακόπτης δ είναι ανοικτός. Κλείνουμε το διακόπτη για t=0 και παρατηρούμε ότι το αμπερόμετρο δείχνει σταθερή ένδειξη Ι=0,2Α. i) Να σχεδιάστε δύο ποιοτικά διαγράμματα για τις εντάσεις των ρευμάτων που διαρρέουν τις δυο αντιστάσεις, σε συνάρτηση με το χρόνο. ii) Να υπολογίσετε τις αντιστάσεις R1 και …
Μάι 29
αγωγός ευθύγραμμος
Ο ευθύγραμμος αγωγός AΓ του σχήματος έχει μάζα m=0,2kg, μήκος l=1m και κρέμεται κατακόρυφα από δύο όμοια ελατήρια σταθεράς k=20Ν/m, παραμένοντας σε οριζόντια θέση. Όλο το σύστημα βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο Β=0,1Τ με δυναμικές γραμμές κάθετες στο επίπεδο του σχήματος (στο επίπεδο της σελίδας). Αν ο αγωγός διαρρέεται ρεύμα με φορά από το Α …
Μάι 31
Φυσική Α
allazontas-tin-timi-tis-dinamis-allazoun-ola Αν η δύναμη αλλάξει διεύθυνση Από την ταχύτητα στη δύναμη Ας ελέγξουμε για τριβές και ενέργειες Για επανάληψη 2024 …η μετακίνηση ενός κιβωτίου Η κίνηση και η μέγιστη ταχύτητα σώματος Η μεταβλητή δύναμη αναδεικνύει τις τριβές Μια οριζόντια εκτόξευση σώματος Μια συνάντηση και οι ενέργειες Όταν η τροχιά δεν έχει σταθερή κλίση Τραβώντας ένα …
Μάι 21
Δυο κυκλώματα και το κλείσιμο των διακοπτών
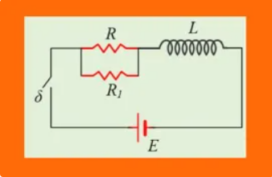
Δίνονται τα κυκλώματα του σχήματος, όπου στο μόνο που διαφέρουν είναι ο αντιστάτης R1 στο 2ο σχήμα, σε παράλληλη σύνδεση με τον αντιστάτη R. Σε μια στιγμή κλείνουμε τους δύο διακόπτες, και μετά από λίγο οι δυο πηγές διαρρέονται από ρεύματα με σταθερές εντάσεις. i) Αν Ε1 και Ε2 οι μέγιστες ΗΕΔ από αυτεπαγωγή (κατ’ απόλυτο τιμή) που αναπτύσσονται …
Ιαν 03
ενέργειες
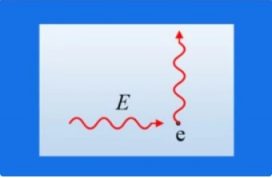
1) Ένα φωτόνιο με ενέργεια Ε=6.000eV προσπίπτει σε ακίνητο ελεύθερο ηλεκτρόνιο. Μετά την αλληλεπίδραση φωτονίου – ηλεκτρονίου, το φωτόνιο συνεχίζει διαδιδόμενο στην ίδια διεύθυνση. Να υπολογιστούν η ενέργεια και η ορμή φωτονίου και ηλεκτρονίου, μετά την αλληλεπίδραση. Δίνεται c=3∙108m/s. 2) Φωτόνια με ενέργεια Ε=6.000eV προσπίπτουν σε ακίνητα και ελεύθερα ηλεκτρόνια. i) Για την περίπτωση σκέδασης …
Μάι 18
Η περιστροφή δύο ράβδων
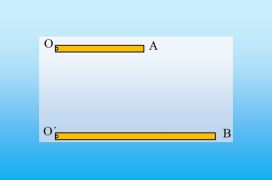
Οι δύο ομογενείς ράβδοι του σχήματος, μπορούν να στρέφονται γύρω από σταθερούς οριζόντιους άξονες, οι οποίοι περνούν από τα άκρα τους Ο και Ο΄, διαγράφοντας κατακόρυφο επίπεδο. Φέρνουμε τις ράβδους σε οριζόντια θέση και τις αφήνουμε να κινηθούν. i) Μεγαλύτερη αρχική επιτάχυνση αποκτά: α) Το άκρο Α της μικρότερης ράβδου. β) Το άκρο Β της …
- 1
- 2



Πρόσφατα σχόλια