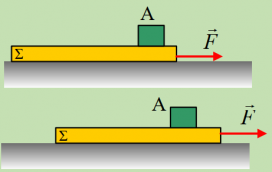
Σε λείο οριζόντιο επίπεδο ηρεμεί μια σανίδα μάζας Μ=3kg, πάνω στην οποία ηρεμεί ένα σώμα Α μάζας m=2kg. Σε μια στιγμή t0=0, στη σανίδα ασκείται μια σταθερή οριζόντια δύναμη F, μέτρου F=6Ν, όπως στο σχήμα. Παρατηρούμε ότι το σώμα Α αρχίζει να γλιστράει πάνω στη σανίδα, ενώ κινείται και αυτό προς τα δεξιά.
i) Να εξηγήσετε, πώς μπορεί να επιταχύνεται προς τα δεξιά το σώμα Α.
ii) Να υπολογισθεί ο ρυθμός μεταβολής της ορμής του συστήματος (σώμα Α-σανίδα), καθώς και η ολική ορμή του συστήματος τη
χρονική στιγμή t1=3s.
iii) Αν τη στιγμή t1 το σώμα Α έχει ταχύτητα υ1=3m/s, να βρεθούν για τη στιγμή αυτή:
α) Η ταχύτητα της σανίδας.
β) Το μέτρο της τριβής που αναπτύσσεται μεταξύ σώματος Α και σανίδας.
iv) Τη στιγμή t1 παύει να ασκείται στη σανίδα η δύναμη F, με αποτέλεσμα μετά από λίγο το σώμα Α να αποκτά την ίδια ταχύτητα με τη σανίδα, ενώ συνεχίζει να βρίσκεται πάνω της. Να υπολογιστεί η κοινή αυτή ταχύτητα των δύο σωμάτων.
ή
και εδώ
