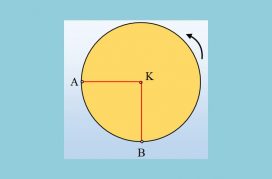
Μια μικρή σφαίρα είναι δεμένη στο άκρο νήματος διαγράφοντας οριζόντιο κύκλο κέντρου Ο, όπως στο σχήμα (κάτοψη), πάνω σε λείο οριζόντιο επίπεδο. Κάποια στιγμή t0=0 η σφαίρα περνά από το σημείο Α, ενώ εκτελεί ομαλή κυκλική κίνηση με συχνότητα f=0,25Ηz.
i) Να υπολογιστεί η γωνία που διαγράφει η σφαίρα μέχρι τη στιγμή t1=15s, βρίσκοντας και την θέση της την στιγμή αυτή.


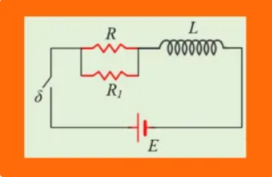







 Σε ευθύγραμμο δρόμο κινούνται με σταθερές ταχύτητες υ1=78km/h και υ2=108km/s, δύο αυτοκίνητα και σε μια στιγμή t=0 μπαίνουν ταυτόχρονα...
Σε ευθύγραμμο δρόμο κινούνται με σταθερές ταχύτητες υ1=78km/h και υ2=108km/s, δύο αυτοκίνητα και σε μια στιγμή t=0 μπαίνουν ταυτόχρονα...