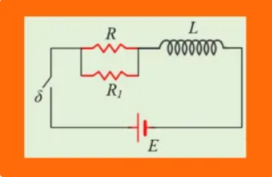
Δίνονται τα κυκλώματα του σχήματος, όπου στο μόνο που διαφέρουν είναι ο αντιστάτης R1 στο 2ο σχήμα, σε παράλληλη σύνδεση με τον αντιστάτη R.
Σε μια στιγμή κλείνουμε τους δύο διακόπτες, και μετά από λίγο οι δυο πηγές διαρρέονται από ρεύματα με σταθερές εντάσεις.
i) Αν Ε1 και Ε2 οι μέγιστες ΗΕΔ από αυτεπαγωγή (κατ’ απόλυτο τιμή) που αναπτύσσονται στα δύο πηνία, θα ισχύει:
α) Ε1 < Ε2, β) Ε1 = Ε2, γ) ) Ε1 > Ε2.
ii) Αν U1 και U2 οι ενέργειες των μαγνητικών πεδίων, που τελικά αποθηκεύονται στα δύο πηνία, θα ισχύει:
α) U1 < U2, β) U1 = U2, γ) ) U1 > U2.






 Σε ευθύγραμμο δρόμο κινούνται με σταθερές ταχύτητες υ1=78km/h και υ2=108km/s, δύο αυτοκίνητα και σε μια στιγμή t=0 μπαίνουν ταυτόχρονα...
Σε ευθύγραμμο δρόμο κινούνται με σταθερές ταχύτητες υ1=78km/h και υ2=108km/s, δύο αυτοκίνητα και σε μια στιγμή t=0 μπαίνουν ταυτόχρονα...
https://1.bp.blogspot.com/-6zBP1lYt3_M/YT2PwrotVFI/AAAAAAAALq4/NYjzXrrfaP0kHBbMbS1WeWCI1MpnjJdEQCLcBGAsYHQ/s320/%25CF%2584655.JPG