Τρίτη 20 Ιανουαρίου
Γλώσσα
Γράψαμε διαγώνισμα. Δεν έχουμε ασκήσεις για το σπίτι.
Μαθηματικά
Αύριο θα γράψουμε διαγώνισμα στις εξισώσεις. Κάνουμε τις ασκήσεις στο φύλλο εργασίας, κάνουμε επανάληψη από το βιβλίο μας και παίζουμε τα παιχνίδια.
- Φύλλο εργασίας: https://files.e-me.edu.gr/s/nGksxXwXRwRZxPZ
- Παιχνίδια εξάσκησης:
- Γράψτε τον αριθμό που λύνει την εξίσωση: https://wordwall.net/resource/105868799
- Βρίσκουμε την εξίσωση που λύνει το πρόβλημα: https://wordwall.net/resource/105869344
- Βοήθεια για τις ασκήσεις θα βρείτε εδώ.
- Εξασκηθείτε μόνοι σας: Αν θέλετε να κάνετε εξάσκηση στις εξισώσεις μόνοι σας, μπορείτε να γράψετε εξισώσεις με όλες τις πράξεις στο τετράδιό σας και να τις λύσετε. Όσοι θέλετε στείλτε μου φωτο στο email (geomihailidis@gmail.com) ή στον Τοίχο. Θα τις ελέγξω και θα σας απαντήσω αν είναι σωστές ή όχι.
- Μπράβο για την προσπάθεια (σε όλους)!
Φυσική
- Κεφάλαιο: Οικονομία στη χρήση ενέργειας
- Ξεκινήσαμε το κεφάλαιο. Θα το ολοκληρώσουμε αύριο, οπότε δεν έχουμε εργασίες για το σπίτι.
Δευτέρα 19 Ιανουαρίου
Γλώσσα
Κάναμε επανάληψη στα γλωσσικά φαινόμενα που συναντήσαμε στην 7η ενότητα. Αύριο θα γράψουμε διαγώνισμα. Αν δεν το έχετε κάνει ήδη ή αν δεν άνοιγαν, δοκιμάστε να παίξετε τα παιχνίδια που έχω ανεβάσει κάνοντας κλικ εδώ.
Μαθηματικά
Κάναμε επανάληψη στις εξισώσεις. Έχουμε για αύριο το παρακάτω φύλλο εργασίας: https://files.e-me.edu.gr/s/5yaSLek9eMZXXNB
Δεν ανεβάζω καμία βοήθεια. Θέλω να δείτε τις ασκήσεις με εξισώσεις που έχουμε κάνει και να προσπαθήσετε να λύσετε τις εξισώσεις της πρώτης σελίδας βήμα-βήμα μόνοι σας. Πρέπει να καταλάβετε με ποια πράξη λύνουμε κάθε εξίσωση ανάλογα με τον αριθμό που είναι άγνωστος.
Ιστορία
Δεν προλάβαμε να προχωρήσουμε. Έχουμε το ίδιο μάθημα για την επόμενη φορά ("Η επανάσταση στα νησιά του Αιγαίου").
Γλώσσα – Ενότητα 7 – Επανάληψη
Παρακάτω θα βρείτε ασκήσεις και παιχνίδια επανάληψης. Κάντε τα με υπομονή και προσοχή (ειδικά το πρώτο, το Λεξιλόγιο θέλει λίγη ώρα για να βρείτε τις σωστές σημασίες.
- Λεξιλόγιο: https://wordwall.net/resource/105707727
- Μετοχές
- Πώς γράφονται: η προηγούμενη: https://wordwall.net/resource/105515131
και καινούργια: https://wordwall.net/resource/105708941 - Ξεχωρίζουμε τις μετοχές Ενεργητικής από τις μετοχές Παθητικής φωνής: η προηγούμενη: https://wordwall.net/resource/105515297
και καινούργια: https://wordwall.net/resource/105709046 - Μετοχές Παθητικής Φωνής με 1 ή 2 μ (-μένος vs. -μμένος): https://wordwall.net/resource/105708522
- Πώς γράφονται: η προηγούμενη: https://wordwall.net/resource/105515131
- Ονοματικές - ρηματικές φράσεις
- Εντοπίζουμε το είδος των φράσεων (αν είναι ρηματικές ή ονοματικές): https://wordwall.net/resource/105708696
- Μετατροπή ονοματικών σε ρηματικές και αντίστροφα: https://wordwall.net/resource/29450070
- Επίθετα σε -ης -ης -ες (διγενή και τρικατάληκτα)
- Τα μεταφέρουμε στον άλλο αριθμό: https://wordwall.net/resource/105708800
- Τα χρησιμοποιούμε σε προτάσεις: https://wordwall.net/resource/105708914
- Απλές - Επαυξημένες - Ελλειπτικές - Σύνθετες προτάσεις
- Επανάληψη:
Απλές: έχουν Υποκείμενο + Ρήμα + Αντικείμενο ή Κατηγορούμενο
Επαυξημένες: έχουν Υποκείμενο + Ρήμα + Αντικείμενο ή Κατηγορούμενο + Προσδιορισμούς του τόπου, του χρόνου κ.ά.
Ελλειπτικές: λείπει το Υποκείμενο ή το Ρήμα (πιο σπάνια οι άλλοι κύριοι όροι της πρότασης)
Σύνθετες: Είναι απλές προτάσεις που, όμως, έχουν 2 Υποκείμενα, 2 Αντικείμενα ή 2 Κατηγορούμενα που συνδέονται με το "και". Δηλαδή έχουν τη δομή: Υ και Υ + Ρήμα + Α ή Υ + Ρ + Α και Α
Π.χ., Η Μαρία και η Σοφία είναι φίλες. - Παιχνίδι εξάσκησης: https://wordwall.net/resource/105744870
- Επανάληψη:
- Κυριολεξία - Μεταφορά - Παρομοίωση - Προσωποποίηση
- Παιχνίδι εξάσκησης: https://wordwall.net/resource/105746073
Παρασκευή 16 Ιανουαρίου
Γλώσσα
- Τη Δευτέρα θα γράψουμε επαναληπτικό διαγώνισμα στην 7η ενότητα.
- Φύλλο εργασίας: https://files.e-me.edu.gr/s/toajgKj2wRCn7iz
Ιστορία
- Κεφάλαιο: Η επανάσταση στα νησιά του Αιγαίου
- Φύλλο εργασίας: https://files.e-me.edu.gr/s/Pi9PRQXmiJn65RQ
Πέμπτη 15 Ιανουαρίου
Γλώσσα
- Δεν έχουμε κάτι για αύριο.
Μαθηματικά
- Φύλλο εργασίας: https://files.e-me.edu.gr/s/HsCHHbzTAzTqjRz
- Ας δούμε λίγο τις εξισώσεις της φωτοτυπίας:
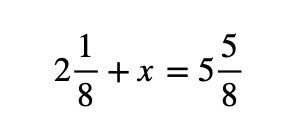
Είναι μία κανονική εξίσωση με πρόσθεση. Απλώς στο πρώτο βήμα θα πρέπει να μετατρέψουμε τους μεικτούς αριθμούς σε κλάσματα. Στη συνέχεια ακολουθούμε τα βήματα με τα οποία λύνουμε τις εξισώσεις με πρόσθεση.
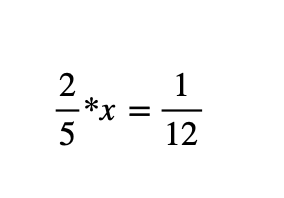
Το σύμβολο * δηλώνει πολλαπλασιασμό. Δυστυχώς στο πληκτρολόγιο δεν μπορώ να βρω κουκίδα και στις φωτοτυπίες μας από εδώ και πέρα θα βάζω αυτό το σύμβολο.
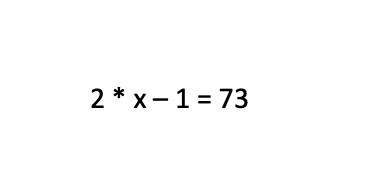
Σε τέτοιες εξισώσεις κάνουμε το εξής: κρατάμε από τη μία πλευρά τις εξίσωσης τους άγνωστους αριθμούς (εδώ 2 * x) και μεταφέρουμε στην άλλη τους γνωστούς κάνοντας τις πράξεις που ταιριάζουν. Άρα, η εξίσωση θα γίνει:
2 * x = 73 + 1
2 * x = 74
Άρα,
χ = 74 : 2
κτλ.
Φυσική
- Ολοκληρώσαμε το κεφάλαιο "Ανανεώσιμες και μη ανανεώσιμες πηγές ενέργειας"
Τετάρτη 14 Ιανουαρίου
Γλώσσα
- Τετράδιο Εργασιών: ασκήσεις 9 και 11, σελ. 59-60.
- τετράδιο Εργασιών Γλώσσας: αναγνωρίζουμε γραμματικά το ρήμα "διαβάζει", όπως στο παράδειγμα που κάναμε στην τάξη.
- Επανάληψη στις μετοχές: https://wordwall.net/resource/105515131 (Διαβάστε τη μετοχή, βάλτε τόνο όπου χρειάζεται, γράψτε το όνομά σας στο Leaderboard)
- Μετοχές Ενεργητικής ή Παθητικής Φωνής; https://wordwall.net/resource/105515297
- Επανάληψη σε ονοματικές-ρηματικές φράσεις: https://wordwall.net/resource/105515018 (γράψτε το όνομά σας στο Leaderboard)
- Επανάληψη στην Ενεργητική - Παθητική φωνή: https://wordwall.net/resource/105514931
- Τι είναι οι συζυγίες των ρημάτων; https://wordwall.net/resource/105515528
Μαθηματικά
- Τετράδιο Εργασιών: ασκήσεις 1-2, προβλήματα 1-2 στη σελ. 27.
Φυσική
- Τετράδιο Εργασιών (πορτοκαλί βιβλίο): Συμπληρώνουμε τον πίνακα στη σελίδα 46 με τις ανανεώσιμες και τις μη ανανεώσιμες μορφές ενέργειας.
Έχετε σκεφτεί ποτέ πώς πραγματικά θα μπορούσαμε να γλιτώσουμε από το να εισάγουμε φυσικό αέριο και πετρέλαιο για τις ενεργειακές μας ανάγκες; Θα μπορούσαμε να παράγουμε εδώ την ενέργεια αυτή; Και αν ναι, πώς θα μας βοηθούσε αυτό σαν χώρα; Θα μπορούσε η Ελλάδα να γίνει δυνατή αν παρήγαγε η ίδια την ενέργεια που χρειάζεται; Σε αυτά και σε άλλα ερωτήματα απαντά η παρουσιάστρια στο βίντεο. Δείτε το! Είναι ενδιαφέρον!
Παιχνίδι για τις ανανεώσιμες και μη ανανεώσιμες πηγές ενέργειας: https://wordwall.net/resource/105514280
Τρίτη 13 Ιανουαρίου
Γλώσσα
- Βιβλίο: άσκηση 9 στη σελίδα 27.
- Τετράδιο Εργασιών: ασκήσεις 1, 4, 5, 6γ και 7.
- Ανάγνωση: το κείμενο για τη μαστίχα (Βιβλίο, σελίδα 26)
Μαθηματικά
- Τετράδιο Εργασιών: ασκήσεις 1, 2 και προβλήματα 1, 3 στις σελίδες 25, 26.
- Βοήθεια για το πρόβλημα 1 δεν ανεβάζω. Θέλω να το προσπαθήσετε μόνοι σας, χωρίς βοήθεια (σκεφτείτε, σκεφτείτε, σκεφτείτε...). Αν φτιάξετε την εξίσωση και θέλετε να μου τη στείλετε να τη δω, μπορείτε είτε στο email μου είτε στον Τοίχο.

Φυσική
- Κεφάλαιο: Φυσικό αέριο - ένα πολύτιμο αέριο
- Εργασίες: 2 και 3 στη σελίδα 40.
Δείτε ένα βίντεο για το πώς σχηματίστηκε το φυσικό αέριο (δυστυχώς στα αγγλικά):
Κι ένα βίντεο για τη διαδικασία εξόρυξης του φυσικού αερίου:
Δευτέρα 12 Ιανουαρίου
Γλώσσα
- Βιβλίο μαθητή: ασκήσεις 5 στη σελίδα 17, 8 και 9 στη σελίδα 19.
- Φύλλο εργασίας (για Απλές, Επαυξημένες, Ελλειπτικές προτάσεις): https://files.e-me.edu.gr/s/qttTmzLjDDjjbrE
- Παιχνίδι για τις απλές-επαυξημένες προτάσεις: https://wordwall.net/resource/105205796
- Παιχνίδι για Κυριολεξία - μεταφορά: https://wordwall.net/resource/105205404
Μαθηματικά
- Τετράδιο Εργασιών: ασκήσεις 1, 2 και προβλήματα 1, 2, 3 στις σελίδες 23-24.
- Παιχνίδι εξάσκησης: https://wordwall.net/resource/105369330
- Βοήθεια για τα προβλήματα:
Πρόβλημα 1
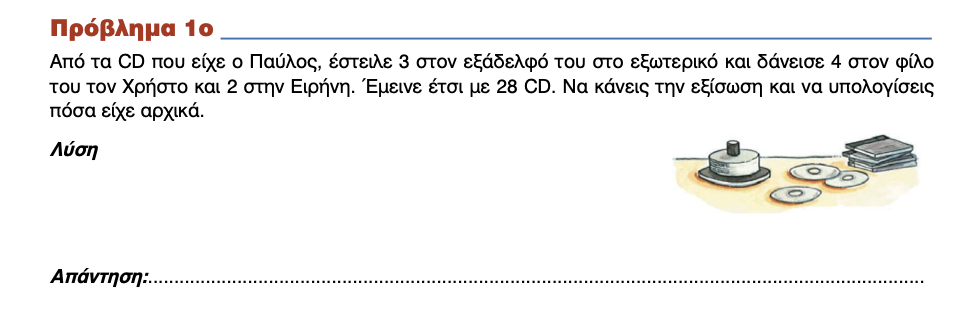
Εδώ πρέπει να σκεφτούμε καταρχήν ποιο γράμμα θα χρησιμοποιήσουμε για τα CD του Παύλου. Ας πούμε ότι θα χρησιμοποιήσουμε το χ.
Θα έχουμε:
χ - {αφαιρούμε επειδή δάνεισε, άρα τα CD του μειώθηκαν)...
χ - (3 + 4 + 2) = {προσθέτουμε τα CD που έδωσε}
χ - (3 + 4 + 2) = 28 {28 του έμειναν αφού δάνεισε}Επόμενο βήμα: κάνουμε τις πράξεις στην παρένθεση:
χ - 9 = 28Και μετά λύνουμε την εξίσωση:
χ = 28 + 9
χ = 37Με τον ίδιο τρόπο λύνουμε το πρόβλημα 2.
Το πρόβλημα 3 είναι εύκολο. Πρέπει απλά να βρούμε αν με χ = 15 η εξίσωση λύνεται.
Ιστορία
- Η επανάσταση στη Στερεά Ελλάδα
- Φύλλο εργασίας: https://files.e-me.edu.gr/s/DiktdFyA5t6icgs
- Ερωτήσεις
- Για ποιους λόγους ήταν δύσκολη η έναρξη της επανάστασης στη Στερεά Ελλάδα;
- Ποιες περιοχές της Στερεάς Ελλάδας επαναστάτησαν τον Μάρτιο και τον Απρίλιο του 1821;
- Τι γνωρίζετε για τη μάχη της Αλαμάνας;
- Τι γνωρίζετε για τη μάχη στο χάνι της Γραβιάς;
Παρασκευή 9 Ιανουαρίου
Γλώσσα
- Φύλλο εργασίας: https://files.e-me.edu.gr/s/oTDq63dR77wb2P5
- Δοκιμάστε να συνδεθείτε στον Τοίχο μας. Εκεί μπορείτε να γράφετε κι εσείς σκέψεις, απόψεις και απορίες και να επικοινωνείτε μεταξύ σας.
- Παιχνίδι για να μάθουμε να αναγνωρίζουμε Κυριολεξία-Μεταφορά: https://wordwall.net/resource/105205404
Ιστορία
- Φύλλο εργασίας: https://files.e-me.edu.gr/s/BzTZAPAwAqzJd5B
Ιστορία – Η εξέγερση στη Μολδοβλαχία
Το Φύλλο εργασίας και οι ερωτήσεις της Ιστορίας για αύριο.
Ιστορία
- Κεφάλαιο: Η εξέγερση στη Μολδοβλαχία
- Φύλλο εργασίας: https://files.e-me.edu.gr/s/Gp9BppTqkr5wqc6
- Ερωτήσεις
- Για ποιους λόγους ξεκίνησε η εξέγερση στη Μολδοβλαχία;
- Ποια ήταν τα κυριότερα γεγονότα της εξέγερσης;
- Ποιο ήταν το τέλος της εξέγερσης;
- Πώς αντέδρασαν οι Μεγάλες Δυνάμεις και ο Τσάρος της Ρωσίας στην εξέγερση στη Μολδοβλαχία; Πώς αντέδρασε ο Πατριάρχης και γιατί;




