Στ1 - 3ο ΔΣ Μαρμάρων

Κλάσματα – Επανάληψη – Παιχνίδια εξάσκησης

1. Βρείτε το ισοδύναμο κλάσμα

2. Κουιζ με ερωτήσεις και ασκήσεις: κάντε κλικ εδώ

Μαθηματικά – Κλάσματα – Όσα πρέπει να ξέρουμε

Για να είμαστε έτοιμοι για το διαγώνισμα, θα πρέπει να είμαστε σίγουροι ότι μπορούμε να κάνουμε σωστά τα παρακάτω:

1. Να μπορούμε να υπολογίσουμε ισοδύναμα κλάσματα
2. Να μπορούμε να μετατρέψουμε κλάσματα σε δεκαδικούς και δεκαδικούς σε κλάσματα
3. Να μπορούμε να απλοποιήσουμε κλάσματα
4. Να μποροούμε να μετατρέψουμε μεικτούς αριθμούς σε καταχρηστικά κλάσματα και το αντίστροφο
5. Να μπορούμε να μετατρέψουμε ετερώνυμα κλάσματα σε ομώνυμα
6. Να μπορούμε να συγκρίνουμε κλάσματα
7. Να μπορούμε να προσθέσουμε και να αφαιρέσουμε κλάσματα (τα έβαλα μαζί γιατί ακολουθούμε την ίδια διαδικασία)
8. Να μπορούμε να πολλαπλασιάσουμε κλάσματα
9. Να ξέρουμε πώς διαιρούμε κλάσματα
10. Να μπορούμε να λύσουμε αριθμητικές παραστάσεις με κλάσματα
11. Να μπορούμε να λύσουμε προβλήματα με πρόσθεση ή και αφαίρεση κλασμάτων
12. Να μπορούμε να λύσουμε προβλήματα με πολλαπλασιασμό ή διαίρεση κλασμάτων

Πάμε να τα δούμε ένα-ένα:

✅ Ισοδύναμα Κλάσματα

Δύο κλάσματα είναι ισοδύναμα αν εκφράζουν την ίδια ποσότητα.

• Πώς το βρίσκω; Πολλαπλασιάζω ή διαιρώ και τους δύο όρους του κλάσματος (αριθμητή και παρονομαστή) με τον ίδιο αριθμό.

• Παράδειγμα:

Τι έκανα; Πολλαπλασίασα αριθμητή και παρονομαστή με τον ίδιο αριθμό (πρώτα το 2 και μετά το 3).

✅ Μετατροπή Κλάσματος σε Δεκαδικό και αντίστροφα

• Κλάσμα σε Δεκαδικό: Διαιρώ τον αριθμητή με τον παρονομαστή.

  •    

    Αν κάνετε τη διαίρεση στο τετράδιό σας θα βρείτε 0,75.

• Δεκαδικός σε Κλάσμα: Γράφω τον αριθμό χωρίς την υποδιαστολή στον αριθμητή. Στον παρονομαστή βάζω το 1 και τόσα μηδενικά όσα ήταν τα δεκαδικά ψηφία.

  •    

✅ Απλοποίηση Κλασμάτων

Κάνουμε το κλάσμα πιο "μικρό" και εύχρηστο.

• Πώς; Διαιρούμε αριθμητή και παρονομαστή με τον Μέγιστο Κοινό Διαιρέτη (Μ.Κ.Δ.) τους. Πώς βρίσκω τον Μ.Κ.Δ.; Δείτε το βίντεο με προσοχή, κάντε δοκιμές (όσες χρειάζεται) στο πρόχειρό σας και θα το μάθετε.

• Παράδειγμα:

     

  Ο Μ.Κ.Δ. (12,16) είναι 4, οπότε διαίρεσα αριθμητή και παρονομαστή με το 4. Αν θέλετε να εξασκηθείτε, απλοποιήστε στο πρόχειρό σας τα κλάσματα 12/15, 20/24, 40/60 μέχρι να γίνουν ανάγωγα (να μην απλοποιούνται άλλο).

✅ Μεικτοί αριθμοί & Καταχρηστικά Κλάσματα

• Μεικτός σε Κλάσμα: Πολλαπλασιάζω τον ακέραιο με τον παρονομαστή και προσθέτω τον αριθμητή. Ο παρονομαστής μένει ίδιος.

• Κλάσμα σε Μεικτό: Κάνω τη διαίρεση. Το πηλίκο είναι ο ακέραιος, το υπόλοιπο είναι ο νέος αριθμητής.

✅ Ετερώνυμα κλάσματα σε Ομώνυμα

• Βήμα 1: Βρίσκω το Ε.Κ.Π. των παρονομαστών.

• Βήμα 2: Βάζω "καπελάκια" πάνω από κάθε κλάσμα και βάζω τον αριθμό που αν πολλαπλασιάσω τον παρονομαστή θα γίνει ίσος με το Ε.Κ.Π.

• Προσοχή: Για να κάνουμε τα κλάσματα ομώνυμα, πρέπει να βρούμε το Ε.Κ.Π. Αν απλώς βάλετε τους παρονομαστές χιαστί στα καπελάκια τα καινούργια κλάσματα θα είναι ομώνυμα, αλλά θα είναι ΤΕΡΑΣΤΙΑ!!!  

• Να η διαδικασία (το βήμα 3 εμείς το έχουμε κάνουμε με τα "καπελάκια"):

✅ Σύγκριση Κλασμάτων

Για να συγκρίνω, πρέπει να τα κάνω Ομώνυμα (με τη διαδικασία που βλέπουμε ακριβώς από πάνω). Μετά, μεγαλύτερο είναι αυτό με τον μεγαλύτερο αριθμητή.

2. Πράξεις με Κλάσματα

➕➖ Πρόσθεση και Αφαίρεση

ΠΡΟΣΟΧΗ: Μπορώ να προσθέσω ή να αφαιρέσω ΜΟΝΟ Ομώνυμα κλάσματα.

1. Αν είναι ετερώνυμα, τα κάνω πρώτα ομώνυμα (με τη διαδικασία που είδαμε παραπάνω).

2. Προσθέτω ή αφαιρώ τους αριθμητές.

3. Ο παρονομαστής μένει ο ίδιος.

✖️ Πολλαπλασιασμός

Εδώ είναι εύκολα τα πράγματα! Δεν χρειάζεται να είναι ομώνυμα.

1. Πολλαπλασιάζω Αριθμητή με Αριθμητή.

2. Πολλαπλασιάζω Παρονομαστή με Παρονομαστή.

➗ Διαίρεση

Θυμήσου τον κανόνα: "Αντιστρέφω και Πολλαπλασιάζω".

1. Αφήνω το πρώτο κλάσμα όπως είναι.

2. Μετατρέπω τη διαίρεση σε πολλαπλασιασμό.

3. Αντιστρέφω το δεύτερο κλάσμα.

🔢 Αριθμητικές Παραστάσεις

Ακολουθώ τη σωστή σειρά ("προτεραιότητα πράξεων"):

1. Παρενθέσεις

2. Πολλαπλασιασμοί & Διαιρέσεις (από αριστερά προς τα δεξιά)

3. Προσθέσεις & Αφαιρέσεις

Παράδειγμα αριθμητικής παράστασης

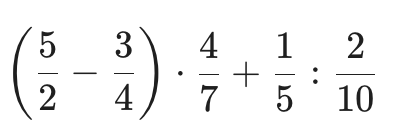
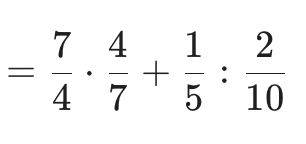
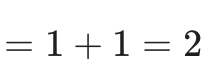
Αν δεν καταλαβαίνετε κάτι, κάντε αναλυτικά τις πράξεις στο τετράδιό σας και θα δείτε ότι θα βρείτε το ίδιο.

3. Λύνοντας Προβλήματα με κλάσματα

Πώς καταλαβαίνω τι πράξη πρέπει να κάνω;

• Πρόσθεση: Όταν ακούω λέξεις όπως "συνολικά", "όλα μαζί".

• Αφαίρεση: Όταν ψάχνω το "υπόλοιπο", τη "διαφορά", το "πόσο παραπάνω/λιγότερο".

• Πολλαπλασιασμός:

  • Όταν ψάχνω μέρος ενός αριθμού (π.χ., το 1/3​ των 60 ευρώ → 1/3​⋅60/1 = 20 ευρώ).

  • Όταν ξέρω την τιμή της μίας μονάδας (ενός συνόλου) και ψάχνω την τιμή του μέρους.

  • Παράδειγμα: Ο Θοδωρής σκόραρε 36 πόντους σε έναν αγώνα μπάσκετ. Από αυτούς τα 3/4 τους σκόραρε με τρίποντα. Πόσους πόντους σημείωσε με τρίποντα; --> Ξέρω το σύνολο των πόντων του Θοδωρή (τα 4/4) και ψάχνω τα 3/4. Θα κάνω πολλαπλασιασμό: 36 $\cdot$ 3/4 και θα βρω τους πόντους του Θοδωρή.

    Β΄ τρόπος: "Ξαναχτίζω" το πρόβλημα, όπως είδαμε σήμερα στην τάξη
    Τα 4/4 των πόντων του Θοδωρή είναι 36
    Το 1/4 των πόντων του Θοδωρή είναι 36 : 4 = 9 πόντοι
    Τα 3/4 των πόντων του Θοδωρή θα είναι 9 x 3 = 27

    Είναι λογική η απάντηση; Αν όλοι οι πόντοι που σκόραρε ο Θοδωρής είναι 36, τότε τα 3/4 των πόντων του είναι 27.

• Διαίρεση:

  • Όταν μοιράζω κάτι σε ίσα μέρη.

  • Όταν θέλω να δω "πόσες φορές χωράει" το ένα στο άλλο.

  • Όταν ξέρω την τιμή του κλάσματος και ψάχνω τη μονάδα (ή όλο τον πληθυσμό).

  • Παράδειγμα: Τα 3/8 των παικτών του Παναθηναϊκού προέρχονται από την Ευρώπη και είναι 12 ποδοσφαιριστές. Πόσοι είναι οι ποδοσφαιριστές του Παναθηναϊκού; Ξέρω τα 3/8 πόσοι παίκτες είναι και ψάχνω τα 8/8, όλους τους παίκτες. Θα κάνω διαίρεση:
    12 : 3/8Β΄ τρόπος: "Ξαναχτίζω" το πρόβλημα, όπως είδαμε σήμερα στην τάξη
    Τα 3/8 των παικτών είναι 12
    Το 1/8 των παικτών είναι 12 : 3 = 4 παίκτες
    Τα 8/8 των παικτών είναι 4 x 8 = 32 παίκτες

    Είναι λογική η απάντηση; Αν όλοι οι τα 3/8 των παικτών είναι 12, τότε όλοι είναι 32. Μια χαρά λογική είναι η απάντησή μας.

Πέμπτη 18 Δεκεμβρίου

Αύριο θα γράψουμε Διαγώνισμα στα Μαθηματικά, στα κεφάλαια 19-24 (κλάσματα). Κάνουμε μία πολύ καλή επανάληψη σε ό,τι είδαμε στα συγκεκριμένα κεφάλαια. 

Γλώσσα

• τετράδιο Εργασιών Γλώσσας: κλίνουμε τα επίθετα "ο συνεχής", "ο διαρκής", "ο επιμελής" στα τρία γένη. Τα επίθετα κλίνονται σαν το "ευτυχής" που γράψαμε στο βιβλίο.

Μαθηματικά

• Φύλλο εργασίας (τις τελευταίες δύο σελίδες): https://files.e-me.edu.gr/s/HHH8zodTmcEddgp
  Λύστε τις ασκήσεις και τα προβλήματα με προσοχή. Αν τα κάνετε βήμα-βήμα, δε θα δυσκολευτείτε. Βοήθεια θα βρείτε στις ασκήσεις που λύσαμε στο τετράδιο στο σχολείο.

Φυσική

• Κεφάλαιο: Πετρέλαιο - Από το υπέδαφος στο σπίτι μας
• Εργασίες: 1-3, σελίδα 27.

Προετοιμασία για διαγώνισμα στα κλάσματα.

Βοήθεια για τα Μαθηματικά

1. Στην άσκηση 1 πρέπει να φτιάξουμε ισοδύναμα κλάσματα. Βλέπουμε, π.χ., ότι το 1/6 = 3/18, επειδή πολλαπλασιάσαμε αριθμητή και παρονομαστή με το 3. Το ίδιο κάνουμε και με τους άλλους δύο αριθμούς.

2. Εδώ τα πράγματα είναι λίγο πιο δύσκολα.
Τα 7/9 είναι εύκολα. Το ίδιο και το επόμενο κλάσμα, τα 2 3/4. Συμπληρώνουμε το 2 και φτιάχνουμε ισοδύναμο κλάσμα με τα 3/4. Φροντίζουμε να πολλαπλασιάζουμε με τον ίδιο αριθμό τον αριθμητή και τον παρονομαστή.

Λίγο πιο δύσκολα εδώ είναι τα 15/20. Σε αυτή την περίπτωση θα βοηθήσει να απλοποιήσουμε πρώτα το κλάσμα (διαιρώντας αριθμητή και παρονομαστή με τον Μ.Κ.Δ. που είναι το 5) και στη συνέχεια να υπολογίσουμε το ισοδύναμο κλάσμα με αριθμητή το 9.

3. Για να φτιάξουμε ανάγωγα κλάσματα, πρέπει να υπολογίσουμε τον Μέγιστο Κοινό Διαιρέτη, τον αριθμό, δηλαδή, που διαιρεί αριθμητή και παρονομαστή. Στη συνέχεια διαιρούμε αριθμητή και παρονομαστή με τον Μ.Κ.Δ. Τα νέα κλάσματα είναι ανάγωγα.

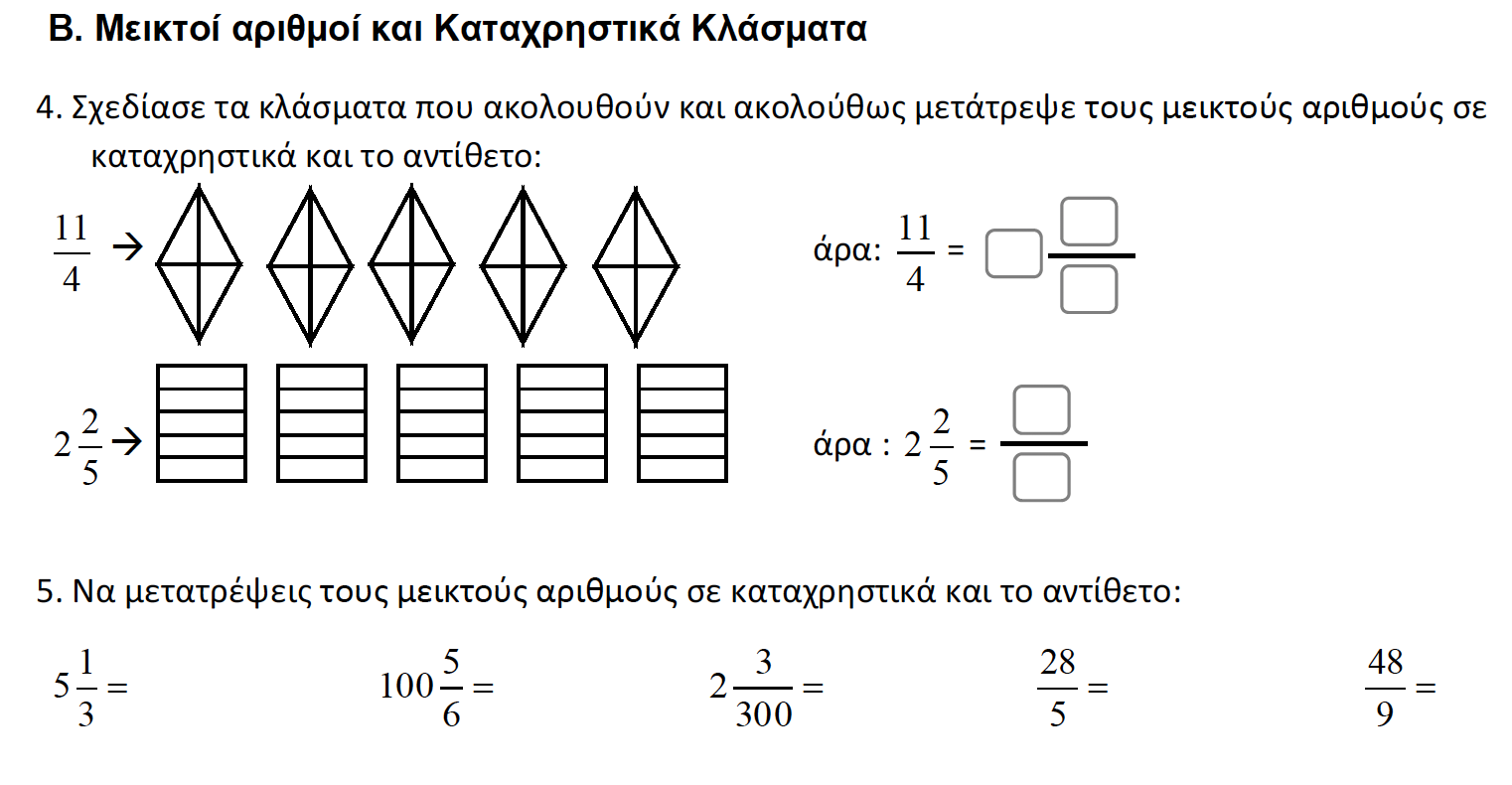
Ακολουθούμε τους τρόπους που ξέρουμε και κάνουμε τις μετατροπές. Ένα παράδειγμα εδώ:

$\displaystyle
\begin{array}{l}
5\frac{1}{3} =\frac{5x3+1}{3} = \frac{16}{3}
\end{array}
$

Υπολογίστε με τον ίδιο τρόπο τα υπόλοιπα.

Δε με νοιάζει τόσο να φαίνεται ο τρόπος σκέψης σας, αλλά θέλω να μπορείτε να δικαιολογήσετε τις απαντήσεις σας. Θυμηθείτε:

α) αν οι αριθμητές είναι ίδιοι, μεγαλύτερο είναι το κλάσμα με τον μικρότερο παρονομαστή (επειδή τα κομμάτια είναι μεγαλύτερα),

β) αν οι παρονομαστές είναι διαφορετικοί, μπορούμε να κάνουμε τα κλάσματα ομώνυμα, ξεκινώντας τη διαδικασία με τα τρία βήματα (πρώτα υπολογίζουμε το Ε.Κ.Π. κτλ.)

Μην ψάχνετε! Κάντε τα ομώνυμα. Ειδικά στα δεύτερα (1/2, 5/6 κτλ.), το Ε.Κ.Π. είναι εύκολο.

Με τον τρόπο που σας έδειξα στο σχολείο:

• Ξέρουμε ότι όλα τα χρήματα (τα 5/5) είναι 240€.
• Ψάχνουμε τα 2/5
• Κάνουμε: Πολλαπλασιασμό 

{Γιατί όταν ξέρουμε το πόσα είναι όλα τα χρήματα και ψάχνουμε ένα μέρος τους κάνουμε πολλαπλασιασμό}

Έτσι θα βρούμε πόσα ξόδεψε τη Δευτέρα.

Με τον ίδιο τρόπο υπολογίζουμε πόσα είναι τα 3/8 των χρημάτων του. Άρα, τι πράξη θα κάνουμε; Τα υπόλοιπα κάντε τα μόνοι σας.

Θα σας δείξω όμως εδώ και έναν τρόπο που θα δούμε αύριο μαζί στο σχολείο. Λοιπόν:

• Τα 5/5 των χρημάτων του είναι 240€
• Το 1/5 των χρημάτων του θα είναι 240 : 5 = 48€ (κάνω διαίρεση, επειδή ξέρω τα πολλά [τα 5/5] και ψάχνω το 1 [το 1/5])
• Τα 2/5 των χρημάτων του θα είναι 48 x 2 = 96€ (κάνω πολλαπλασιασμό, επειδή ξέρω το 1 [το 1/5] και ψάχνω τα πολλά [τα 2/5])

Λύση

• Ξέρω ότι τα 3/7 είναι 120 αγόρια
• Ψάχνω τα 7/7.
• Πράξη: Διαίρεση

Με τον αυριανό τρόπο:

• Τα 3/7 είναι 120 αγόρια
• Το 1/7 είναι 120 : 3 = 40 παιδιά
• Τα 7/7 (όλα τα παιδιά) είναι: 40 x 7 =280 παιδιά

Εδώ πρέπει καταρχήν να βρούμε τι μέρος του συνόλου είναι τα παιδιά. Διαβάστε παρακάτω με προσοχή και σκεφτείτε μαζί μου:

• Θα πρέπει να βρούμε πόσες είναι μαζί οι γυναίκες και οι άνδρες. Για να το υπολογίσουμε αυτό θα κάνουμε πρόσθεση. Αν κάνουμε σωστά τις πράξεις, θα βρούμε ότι είναι τα 7/10. Άρα, τα παιδιά είναι ... (τι θα κάνω για να το βρω;) Θέλω να το σκεφτείτε μόνοι σας και να μου πείτε αύριο την απάντησή σας.
• Οι γυναίκες είπαμε ότι είναι τα 3/5 των θεατών. Μας λέει το πρόβλημα ότι είναι 90.
• Άρα, τα 3/5 είναι 90. Πώς θα υπολογίσουμε τα 5/5;

Λύνουμε τις αριθμητικές παραστάσεις βήμα-βήμα, με τη σειρά που έχουμε δει ότι κάνουμε τις πράξεις. Ξέρουμε πώς κάνουμε προσθέσεις και αφαιρέσεις. Απλώς, αν έχουμε παρένθεση, κάνουμε πρώτα τις πράξεις μέσα σε αυτήν.

Η λύση είναι:

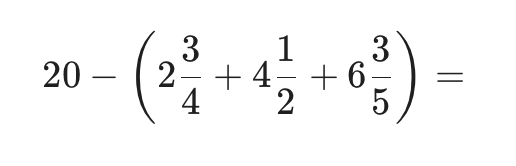
Κάντε μία-μία τις πράξεις και θα το λύσετε.

Τετάρτη 17 Δεκεμβρίου

Γλώσσα

Κάναμε με τη φοιτήτρια. Θυμηθήκαμε τι είναι οι μετοχές (ενεργητικής και παθητικής φωνής) και πώς σχηματίζονται, τα δύσκολα επίθετα σε -ης -ης -ες (ο διεθνής - η διεθνής - το διεθνές) και τις ονοματικές-ρηματικές φράσεις.

Μαθηματικά

• Φύλλο εργασίας: μπορούμε να το βρούμε εδώ: https://app.box.com/s/zl3ro18u0juyuyng8d4qhe1iawvc33l5
  Η φωτοτυπία που πήραμε στο σχολείο έχει δύο ακόμη σελίδες, τις οποίες δε χρειάζεται να κάνουμε. Θα τις κάνουμε αύριο στο σχολείο.

Φυσική

Δεν προλάβαμε να κάνουμε.

Επείγουσα ανακοίνωση

Αύριο δεν έχουμε σχολείο, επειδή συμμετέχω στην απεργία που έχει προκηρύξει η ΔΟΕ για την ψήφιση του προϋπολογισμού. Τα παιδιά που θα δείτε αυτό το μήνυμα ενημερώστε -σας παρακαλώ- και τα άλλα παιδιά, ώστε να μην έρθουν το πρωί στο σχολείο.

Πέμπτη 11 Δεκεμβρίου

Την Τρίτη περιμένω από όλους τα μπλοκ των Εικαστικών. Θέλω κι εγώ να δω τι -από όσα έργα σας έδειξε η κυρία Ελένη των Εικαστικών- κάνατε! Αν χρωστάτε κάποια έργα, σας προτείνω να τα κάνετε. 

Γλώσσα

• Ανάγνωση: "Ολική καταστροφή στις καλλιέργειες" (Βιβλίο μαθητή, τεύχος 2, σελ. 8). Μπορούμε να το βρούμε εδώ: https://ebooks.edu.gr/ebooks/v/html/8547/2005/Glossa_ST-Dimotikou_html-empl/index2_01.html
• Φύλλο εργασίας: ερωτήσεις κατανόησης και λεξιλογίου: https://files.e-me.edu.gr/s/tSR7AjkcRHQoJcx

Μαθηματικά

Δεν έχουμε τίποτα. Όσα παιδιά θέλουν να γίνουν καλύτερα στα κλάσματα που κάνουμε αυτές τις μέρες, μπορούν να λύσουν στο τετράδιο Μαθηματικών τις αριθμητικές παραστάσεις που θα βρουν στο παρακάτω φυλλάδιο: https://files.e-me.edu.gr/s/QMPKZwx9PjSdbmR

Φυσική

• Κεφάλαιο: Πηγές ενέργειας
• Φύλλο εργασίας: https://youtu.be/Be0AWtqZFmg?si=JrXAb5F8tt9RSyWq
• Το Φύλλο Εργασίας βασίζεται στο παρακάτω βίντεο. Δείτε το για να μπορέσετε να απαντήσετε στις ερωτήσεις.

Μαθηματικά – 24. Προβλήματα με πολλαπλασιασμό και διαίρεση κλασμάτων – Τετράδιο Εργασιών – Πρόβλημα 3

Λοιπόν, πληροφορία 1η: Ο κ. Γεωργιάδης κράτησε το 1/3 για τον εαυτό του και μοίρασε τα υπόλοιπα χρήματα στα 3 παιδιά του. Πόσα ήταν τα υπόλοιπα χρήματα;

Αν όλα τα χρήματα ήταν 3/3, τότε τα υπόλοιπα ήταν:

Πολύ ωραία! Τώρα αυτά τα 2/3 τα μοίρασε στα 3 παιδιά του. Λέξη κλειδί; Τι πράξη θα κάνουμε;

1η Απάντηση: 2/9 των συνολικών χρημάτων πήρε κάθε παιδί. 

Πάμε τώρα στο άλλο ερώτημα:

Είπαμε πως τα παιδιά πήραν τα 2/3. Μας λέει το πρόβλημα πως τα 2/3 ήταν 1.800 €. Πόσο ήταν το συνολικό ποσό (τα 3/3);

Ξέρω το μέρος (τα 2/3) και ψάχνω το όλο (τα 3/3). Τι πράξη θα κάνω;

α) Πολλαπλασιασμό
β) Διαίρεση, επειδή ψάχνω το συνολικό ποσό.

Νομίζω πως από εδώ και πέρα δε χρειάζεστε βοήθεια...

Τετάρτη 10 Δεκεμβρίου

Ανακοίνωση

Αύριο όλοι πρέπει να φέρετε στο σχολείο το μπλοκ των Εικαστικών μας. Σας το ζήτησε η κυρία των Εικαστικών και μου είπε ότι πολλά παιδιά δεν το είχαν φέρει. Αύριο, λοιπόν, δεν το ξεχνάμε πάλι!

Γλώσσα

Γράψαμε διαγώνισμα, οπότε δεν προχωρήσαμε παρακάτω. Για αύριο διαβάζουμε 5 (ή περισσότερες σελίδες) από το βιβλίο μας.

Μαθηματικά

Στην τάξη είδαμε δύο πράγματα σήμερα:

α) Πώς διαιρούμε κλάσματα. Είπαμε ότι για να διαιρέσουμε δύο κλάσματα: αντιστρέφουμε το δεύτερο (τον διαιρέτη) και κάνουμε πολλαπλασιασμό:

Δείτε τι κάναμε: κάναμε τη διαίρεση πολλαπλασιασμό και αντιστρέψαμε τα 5/7 (τα κάναμε 7/5). Στη συνέχεια κάναμε τον πολλαπλασιασμό, όπως έχουμε μάθει στα προηγούμενα μαθήματα.

β) Είδαμε πότε λύνουμε ένα πρόβλημα με κλάσματα κάνοντας διαίρεση. Είδαμε ότι κάνουμε διαίρεση σε δύο περιπτώσεις:

1. όταν θέλουμε να μοιράσουμε μία ποσότητα. Παράδειγμα: Μοιράσαμε 17 λίτρα νερό σε μπουκάλια που χωράνε 1/2 λίτρα το καθένα. Πόσα μπουκάλια γεμίσαμε;
2. όταν ξέρουμε το μέρος (το κλάσμα) και ψάχνουμε το όλο. Πέρυσι ο Ιωαννίδης έβαλε 12 γκολ που ήταν τα 2/7 των γκολ που έβαλε συνολικά ο Παναθηναϊκός. Πόσα γκολ έβαλε συνολικά ο Παναθηναϊκός;
   Σκέφτομαι: Ξέρω τα 2/7 ότι είναι 12 γκολ. Ψάχνω πόσα είναι όλα τα γκολ (τα 7/7). Άρα, θα κάνω διαίρεση.

• Αξιοποιώντας τα παραπάνω λύνουμε: την άσκηση 2, τα προβλήματα 2 και 3 στη σελίδα 17 του τετραδίου Εργασιών.
• τετράδιο Μαθηματικών: Λύνουμε την αριθμητική παράσταση:

Η άσκηση 2 είναι αριθμητική παράσταση. Κάνουμε τις πράξεις με τη σειρά που έχουμε πει: πρώτα τους πολλαπλασιασμούς και τις διαιρέσεις και μετά τις προσθέσεις και τις αφαιρέσεις. Όμως, αν έχουμε παρενθέσεις κάνουμε πρώτα τις πράξεις μέσα σε αυτές.

Φυσική

• Κεφάλαιο: Πηγές ενέργειας
• Στο σχολείο συμπληρώσαμε την πρώτη παρατήρηση, για τον ήλιο, που είναι η βασική πηγή ενέργειας του πλανήτη μας. Γράψαμε ότι: Ο ήλιος ακτινοβολεί φως και θερμότητα. Μες την ενέργειά του λειτουργούν ηλιακοί θερμοσίφωνες και φωτοβολταϊκά.

Τρίτη 9 Νοεμβρίου

Γλώσσα

• Φύλλο εργασίας: επανάληψη στην 6η ενότητα: μπορούμε να το βρούμε εδώ: https://files.e-me.edu.gr/s/moNigRZJK6Px2b8

Μαθηματικά

• Τετράδιο Εργασιών: άσκηση 1 και πρόβλημα 1 στη σελίδα 17.

Φυσική

• Κεφάλαιο: Μορφές της ενέργειας
• Τι πρέπει να μάθουμε: α) πρέπει να ξέρουμε τις μορφές της ενέργειας, β) να μπορούμε να βρούμε ποια μορφή ενέργειας έχουμε σε κάθε φαινόμενο (π.χ., στο αυτοκίνητο που κινείται η ενέργεια είναι κινητική, στο τζάκι έχουμε θερμότητα κτλ.).