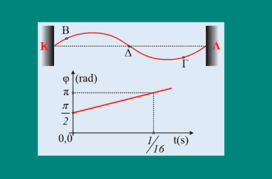
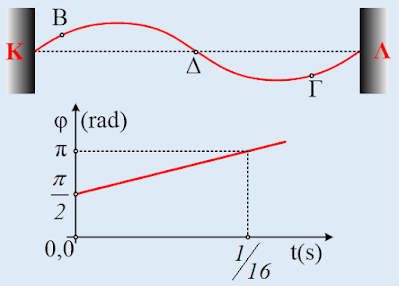
Πάνω σε μια ελαστική χορδή με σταθερά τα δυο της άκρα Κ και Λ, έχει σχηματισθεί ένα στάσιμο κύμα και τη στιγμή t0=0 η μορφή της είναι αυτή του σχήματος, όπου το σημείο Β, το οποίο απέχει οριζόντια απόσταση 0,25m από το άκρο Κ έχει απομάκρυνση yΒ=0,2m (τα θετικά προς τα πάνω) και μηδενική ταχύτητα ταλάντωσης. Στο διάγραμμα δίνεται η φάση της απομάκρυνσης του σημείου Β, σε συνάρτηση με το χρόνο. Δίνεται ότι η ταχύτητα διάδοσης ενός τρέχοντος κύματος κατά μήκος της χορδής αυτής είναι υ=12m/s, ενώ ένα σημείο Ο μεταξύ Κ και Δ, απέχει οριζόντια 0,75m από το Κ.
i) Να υπολογιστεί το μήκος (ΚΛ) της χορδής, τη στιγμή που όλα τα σημεία της περνούν από τη θέση ισορροπίας τους.
ii) Να γίνει η αντίστοιχη γραφική παράσταση της φάσης φ=f(t) για τα σημεία Ο και Γ.
iii) Για να μπορέσουμε να γράψουμε την εξίσωση του στάσιμου κύματος, θεωρούμε ως αρχή του άξονα x τη θέση του σημείου
Ο, με την προς τα δεξιά κατεύθυνση ως θετική.
α) Να βρεθεί το μέγιστο πλάτος του στάσιμου κύματος.
β) Να γράψετε την εξίσωση του στάσιμου κύματος.
ή