Category: Μαθηματικά Στ’ τάξη

Μαθηματικά 15/5: Εκτιμώ το ποσοστό (μέρος β’)

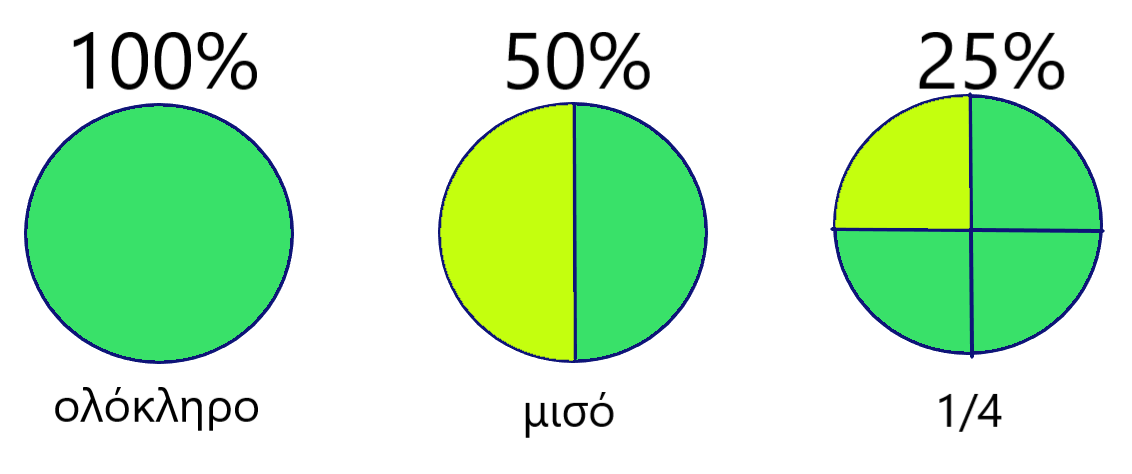
Συνεχίσαμε σήμερα την καλύτερη γνωριμία μας με τα ποσοστά %.

Διαφορετικές εκφράσεις των ποσών.

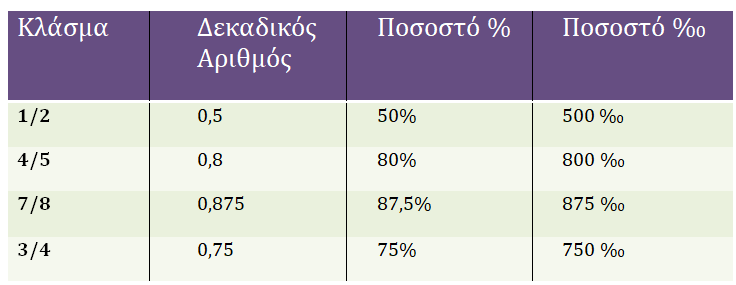
Πώς μετατρέπουμε ένα κλάσμα στα %;

-Φτιάχνω ισοδύναμα κλάσματα με παρονομαστή 100.

-Μετατρέπω το κλάσμα σε δεκαδικό αριθμό και μετά ξανά σε δεκαδικό κλάσμα.

-Λύνω με χιαστί και εξίσωση (όπως στα ανάλογα ποσά)

Έγιναν: Τετράδιο μαθηματικών και Τ.Ε. σελ. 14 ασκ. 4-5, σελ. 15 ασκ. 1

🏡Σπίτι:  ποσοστά ασκήσεις 2

Μαθηματικά 14/5: Εκτιμώ το ποσοστό (μέρος α’)

Σήμερα μπήκαμε σε νέα ενότητα αλλά όχι καινούριες έννοιες.... Ποσοστά!

Τι είναι το ποσοστό;

Το ποσοστό είναι το μέρος ενός συνόλου.

Π.χ. Σε ένα σχολείο όλα τα παιδιά είναι 200. Στην εκδρομή θα έρθουν τα 100 παιδιά.

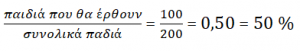.   Θα έρθουν δηλαδή τα μισά παιδιά.

Το πιο γνωστό ποσοστό είναι στα 100 (%).

Βασικά Ποσοστά

Έγιναν: Τ.Ε. (τεύχος γ') σελ. 13-14  ασκ. 1 και τετράδιο μαθηματικών.

🏡Σπίτι: Τ.Ε. (τεύχος γ') σελ. 13-14  ασκ. 2-3-δραστηριότητα με προεκτάσεις

Μαθηματικά 13/5: Επαναληπτική επιστροφή

Καλή μας επιστροφή! Πριν από τις πασχαλινές διακοπές είχαμε ολοκληρώσει τις αναλογίες (ανάλογα και αντιστρόφως ανάλογα ποσά). Προτού προχωρήσουμε σε νέους ορίζοντες, σήμερα φρεσκάραμε λίγο τα προηγούμενα.

Έγιναν: Διορθώσαμε όσα είχαμε για το σπίτι και ασκήσεις στο τετράδιο.

🏡Σπίτι: Ασκήσεις στο τετράδιο (και με τους 3 τρόπους)

  1. Δεκαπέντε μαθητές συνεργάζονται και ποτίζουν τα παρτέρια του σχολείου τους κάνοντας 2 διαδρομές ο καθένας τους. Αν δεν συνεργαστούν και ποτίσουν μόνο ο Θανάσης και ο Λευτέρης όλα τα παρτέρια, πόσες διαδρομές θα κάνουν;
  2. Σε μια κατασκήνωση 120 παιδιά έχουν τρόφιμα για 20 ημέρες. Αν φύγουν το 1/3 των παιδιών, πόσες ημέρες θα περάσουν τα υπόλοιπα παιδιά με τα ίδια τρόφιμα;

 

Μαθηματικά 25/4: Μίξερ ποσών – τιμών (μέρος α’)

Σήμερα μιξάραμε κάνοντας ταυτόχρονα ασκήσεις με ανάλογα και αντιστρόφως ανάλογα ποσά.

Έγιναν: 

🏡Σπίτι: Μελετώ όλα τα προβλήματα που έχουμε λύσει μέχρι τώρα, ώστε να προετοιμαστώ για το παιχνίδι προβλημάτων.

Μαθηματικά 23/4: Αντιστρόφως ανάλογα ποσά (μέρος δ’)

Τελευταίος τρόπος επίλυσης προβλημάτων με αντιστρόφως ανάλογα ποσά: μέθοδος των τριών!

Έγιναν: από φωτοτυπία ασκ. 7-8-9

🏡Σπίτι: Τα υπόλοιπα προβλήματα από ασκήσεις στα αντιστρόφως ανάλογα ποσά

Μαθηματικά 22/4: Αντιστρόφως ανάλογα ποσά (μέρος γ’)

Σήμερα συνεχίσαμε να εξασκούμαστε στην επίλυση προβλημάτων με αντιστρόφως ανάλογα ποσά.

Έγιναν: Τ.Ε. σελ. 11-12 όλα τα προβλήματα

🏡Σπίτι: Τα προβλήματα  1-6 από ασκήσεις στα αντιστρόφως ανάλογα ποσά

Μαθηματικά 19/4: Αντιστρόφως ανάλογα ποσά (μέρος β’)

Σήμερα μελετήσαμε πώς μπορούμε να λύσουμε προβλήματα με αντιστρόφως ανάλογα ποσά.

Έγιναν: τετράδιο μαθηματικών και Τ.Ε. σελ. 7 πρόβλημα 1

🏡Σπίτι: Τα υπόλοιπα προβλήματα από το τε και ασκ 1-2 από ασκήσεις στα αντιστρόφως ανάλογα ποσά

Μαθηματικά 18/4: Αντιστρόφως ανάλογα ποσά (μέρος α’)

Σήμερα μελετήσαμε τα αντιστρόφως ανάλογα ποσά.

Έγιναν: Βιβλίο σελ. 87 και Τ.Ε. (τεύχος β') σελ. 41 ασκ. 1

🏡Σπίτι:

  • Τ.Ε. τεύχος β' σελ. 41 ασκ. 3-πρόβλημα 1
  • Προβλήματα στο τετράδιο
  • Ένα οικόπεδο 400 τ.μ. πουλιέται 48.000 €. Πόσο πρέπει να πουληθεί το διπλανό οικόπεδο που είναι 517 τετραγωνικά μέτρα;
  • Ο Νικολάκης έχει ύψος 1,5 m και το μήκος της σκιάς του είναι 0,75m. Την ίδια στιγμή το μήκος της σκιάς του Στέλιου είναι 0,80 m. Πόσο είναι το ανάστημα του
    Στέλιου;
  • Ένα αυτοκίνητο για 10 km καίει 1 λίτρο βενζίνη.
    α) Πόσα λίτρα βενζίνη θα κάψει σε 17 km;
    β) Πόσα χιλιόμετρα θα διανύσει με 70 km βενζίνη;