Σήμερα ολοκληρώσαμε την επανάληψή μας.

Έγιναν: υπόλοιπες ασκήσεις φωτοτυπίας
Σήμερα ολοκληρώσαμε την επανάληψή μας.

Έγιναν: υπόλοιπες ασκήσεις φωτοτυπίας
Συνεχίσαμε την εξάσκησή μας στην παραγοντοποίηση και μελετήσαμε τον τρόπο με τις διαδοχικές διαιρέσεις.

🏡Έγιναν: Τ.Ε. σελ. 35 άσκηση 4
🏡Σπίτι: παραγοντοποίηση ασκήσεις τις ασκήσεις 1-2-3
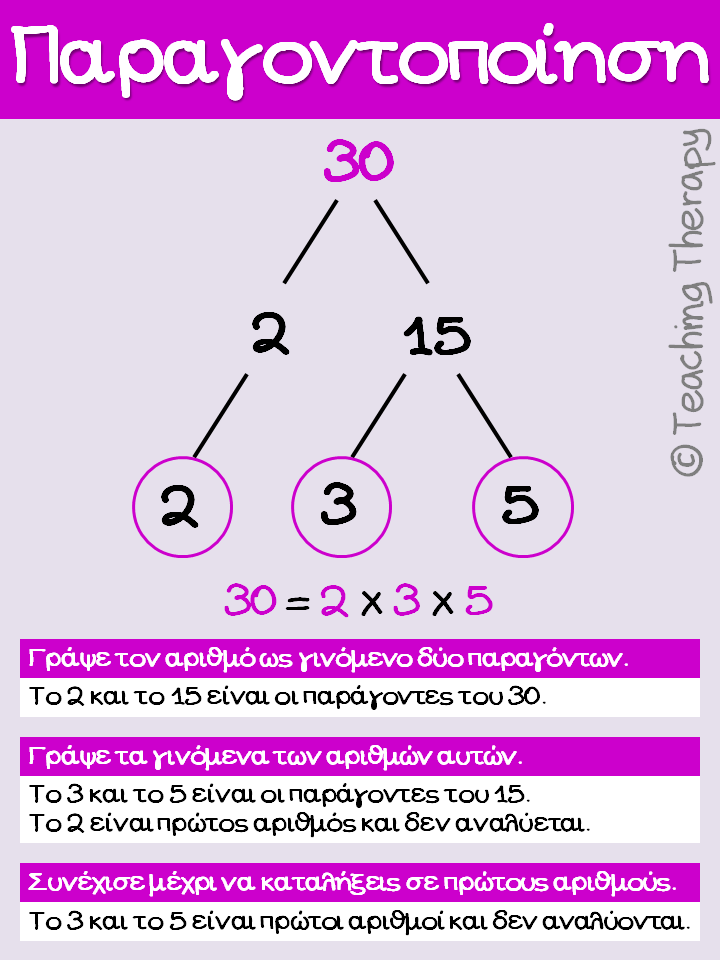
Πώς μπορεί να ένας σύνθετος αριθμός να εκφραστεί γρήγορα και εύκολα σαν γινόμενο πρώτων αριθμών (γινόμενο πρώτων παραγόντων); Με τη διαδικασία της παραγοντοποίησης!
Έγιναν: εξάσκηση στο τετράδιο μαθηματικών τη μέθοδο με το δενδροδιάγραμμα
🏡Σπίτι: Τ.Ε. σελ. 35 ασκ. 1-2-3. Αύριο φέρνω εκτάκτως Μαθηματικά!!!!
Καινούριο μάθημα για σήμερα: Πρώτοι και σύνθετοι αριθμοί

Είναι ένα ειδικό "κόσκινο" που κρατάει όλους τους σύνθετους αριθμούς και αφήνει να περάσουν όλοι οι πρώτοι. Οι αρχαίοι Έλληνες γνώριζαν ότι δεν υπάρχει μέγιστος πρώτος αριθμός, δηλαδή ότι οι πρώτοι αριθμοί είναι άπειροι στο πλήθος. Γνώριζαν ακόμη ότι δεν υπάρχει ένας απλός κανόνας που να δίνει τους διαδοχικούς πρώτους αριθμούς.
Με την απλή μέθοδο του Ερατοσθένη, γνωστή ως "Κόσκινο του Ερατοσθένη", που χρησιμοποιείται μέχρι και σήμερα, βρίσκουμε όλους τους πρώτους αριθμούς που είναι μικρότεροι από δοσμένο αριθμό.

Έγιναν: Βιβλίο σελ. 35 και τετράδιο μαθηματικών
🏡Σπίτι: T.E. σελ. 33 όλες τις ασκήσεις
Στο σημερινό μας μάθημα συνεχίσαμε να εξασκούμαστε στη μέτρηση γωνιών με μοιρογνωμόνιο και πώς μπορούμε να κατασκευάσουμε μια γωνία συγκεκριμένων μοιρών.

Έγιναν: Τ.Ε. (τεύχος δ') σελ. 13 ασκ. 1-2
🏡Σπίτι: ΦΥΛΛΟ-ΕΡΓΑΣΙΑΣ
Σήμερα κάναμε εξάσκηση στα κριτήρια διαιρετότητας και τον ΜΚΔ.

Έγιναν: Τ.Ε. σελ. 29-30 πρόβλημα 1-2-3 και στο τετράδιο μαθηματικών άσκηση διαιρετότητας


Έγιναν: Βιβλίο σελ. 33 και Τ.Ε. σελ. 31 ασκ. 1-2-3
🏡Σπίτι: Τ.Ε. σελ. 31-32 πρόβλημα 1-2
Σήμερα μελετήσαμε στην επίλυση ποιων προβλημάτων είναι χρήσιμος ο Μ.Κ.Δ.

Έγιναν: μέγιστος κοινός διαιρέτης
🏡Σπίτι: δεν έχουμε ασκήσεις. Αύριο φέρνουμε εκτάκτως μαθηματικά!
Σήμερα στα Μαθηματικά μάθαμε τρεις τρόπους για να βρίσκουμε τον ΜΚΔ. Αλλά αρχικά, τι είναι ο Μ.Κ.Δ;

Πώς βρίσκω το ΜΚΔ;
Έγιναν: Βιβλίο σελ. και ασκήσεις στο τετράδιο μαθηματικών
🏡Σπίτι: Βρες το Μ.Κ.Δ. των αριθμών α. 18 , 48 , 72 και β. 100 , 150 , 200 γ.36, 72, 44 δ. 210,220,40 ε. 35,125,200 με τη μέθοδο των διαδοχικών διαιρέσεων (εναλλακτικός τρόπος).

Έγιναν: Βιβλίο σελ. 31 δραστηριότητα 1 και εξάσκηση στο τετράδιο μαθηματικών.
🏡Σπίτι:
α. 12, 24, 60 β. 12, 18, 9 γ. 28, 36, 14 δ. 9, 12, 18 ε. 30, 45, 90