English

Category: Φυσική Γ

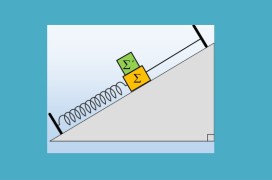
Κινδυνεύουμε να έχουμε ολίσθηση;

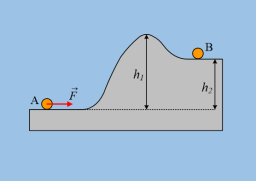
Ένα σώμα Σ μάζας m=1kg ηρεμεί σε λείο κεκλιμένο επίπεδο γωνίας κλίσεως θ=30°, δεμένο στο άκρο ιδανικού ελατηρίου και στο άκρο νήματος, παράλληλου προς το επίπεδο, όπως στο σχήμα. Σε μια στιγμή κόβουμε το νήμα, οπότε το σώμα εκτελεί αατ, με αρχική επιτάχυνση μέτρου |α1|=10m/s2 ενώ ολοκληρώνει πέντε πλήρεις ταλαντώσεις σε χρονικό διάστημα t1=3,14s.

i) Να υπολογιστούν:

 α) το πλάτος της ταλάντωσης του σώματος Σ.

 β) Η τάση Τ1 του νήματος, πριν το κόψουμε.

 γ) Η μέγιστη συσπείρωση του ελατηρίου.

ii) Επαναλαμβάνουμε το πείραμα, αλλά τώρα προσθέτουμε πάνω στο σώμα Σ, ένα δεύτερο σώμα Σ΄ με μάζα επίσης m, το οποίο ισορροπεί.

α) Να υπολογιστεί η τάση του νήματος Τ2.

β) Αν ο συντελεστής οριακής στατικής τριβής μεταξύ των δύο σωμάτων είναι μs=0,8, να εξετάσετε τι πρόκειται να συμβεί, αν κόψουμε το νήμα: Τα δυο σώματα θα ταλαντώνεται μαζί, ή θα υπάρξει ολίσθηση μεταξύ τους.

Δίνεται g=10m/s2, ενώ θεωρούνται γνωστοί οι τριγωνομετρικοί αριθμοί της γωνίας των 30°!!!

Απάντηση:

 ή

Μια ελαστική κρούση και δύο αατ

 

Ένα σώμα Σ1 μάζας m1 είναι δεμένο στο άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=100Ν/m και ταλαντώνεται με εξίσωση x=0,5∙ημ(10t+π/2) (μονάδες στο S.Ι.), με θετική την προς τα δεξιά κατεύθυνση. Ένα δεύτερο σώμα Σ2 μάζας m2=1,5kg κινείται με ταχύτητα υ2 κατά μήκος του άξονα του ελατηρίου, πλησιάζοντας το σώμα Σ1. Αν τη  χρονική στιγμή t0=0 τα δυο σώματα απέχουν απόσταση d1=(π/8+0,5)m, ενώ τα σώματα συγκρούονται κεντρικά και ελαστικά τη χρονική στιγμή t1=π/20 s.

  1. Να υπολογιστεί η μάζα του σώματος Σ1 και η θέση της κρούσης, μεταξύ των δύο σωμάτων.
  2. Να βρεθούν οι ταχύτητες των δύο σωμάτων ελάχιστα πριν την κρούση.
  3. Ποια η μεταβολή της ορμής του σώματος Σ1 που οφείλεται στην κρούση;
  4. Αφού βρείτε τη συνάρτηση x=f(t) για την ταλάντωση του σώματος Σ1 μετά την κρούση, αν αυτή έχει αμελητέα διάρκεια, να γίνει η γραφική παράσταση της απομάκρυνσης του Σ1 σε συνάρτηση με το χρόνο από τη στιγμή t0=0, μέχρι τη στιγμή t2ω= π/4 s.

Απάντηση:

ή

Μια του Αυγούστου

Μια ομογενής ράβδος μήκους ℓ=3m και μάζας Μ=40kg συγκρατείται σε οριζόντια θέση, ενώ ένα τμήμα της μήκους δ=1m στηρίζεται πάνω σε τραπέζι, όπως στο σχήμα. Κάποια στιγμή αφήνουμε ελεύθερη την ράβδο να πέσει και παρατηρούμε ότι στρέφεται γύρω από το άκρο Α του τραπεζιού, μέχρι να στραφεί κατά 12°, αφού στη συνέχεια ολισθαίνει.

  1. Να υπολογιστεί η κινητική ενέργεια της ράβδου, στη θέση που αρχίζει η ολίσθηση.
  2. Πόση είναι η κάθετη αντίδραση του τραπεζιού, στην παραπάνω θέση;
  3. Να υπολογιστεί ο συντελεστής οριακής στατικής τριβής μεταξύ ράβδου και τραπεζιού.

Ένας επιταχυνόμενος δίσκος και οι επιταχύνσεις σημείων

Ένας λεπτός δίσκος, ακτίνας R=0,8m αρχικά ακίνητος σε οριζόντιο επίπεδο, δέχεται κατάλληλη δύναμη οπότε αρχίζει να κυλίεται (χωρίς να ολισθαίνει). Στο πρώτο σχήμα βλέπετε τον κυλιόμενο δίσκο, ενώ στο δεύτερο δίνεται η ταχύτητα του κέντρου του Κ (και κέντρου μάζας του), σε συνάρτηση με το χρόνο. 

  1. Να υπολογιστεί η επιτάχυνση του κέντρου Κ, καθώς και η γωνιακή επιτάχυνση του δίσκου.
  2. Να υπολογιστεί η οριζόντια επιτάχυνση του σημείου Α, πάνω στην κατακόρυφο διάμετρο, το οποίο απέχει κατά (ΚΑ)=r=0,4m από το κέντρο του δίσκου.
  3. Να βρεθεί ποια χρονική στιγμή t1 το σημείο Β, στο άκρο μιας οριζόντιας ακτίνας, έχει κατακόρυφη επιτάχυνση. Πόση είναι τη στιγμή αυτή η επιτάχυνση του σημείου Γ, στο άκρο της κατακόρυφης ακτίνας, σημείο επαφής με το οριζόντιο επίπεδο;

Ταυτόχρονη λειτουργία δύο αντλιών

Στο σχήμα βλέπετε δύο αντλίες οι οποίες «ανακυκλώνουν» το νερό που βρίσκεται σε δοχείο, σε ύψος Η από το έδαφος. Η πρώτη αντλία μεταφέρει το νερό μέσω σωλήνα διατομής S1, ενώ η δεύτερη μέσω σωλήνα διπλάσιας διατομής S2=2S1. Και οι δύο αντλίες βρίσκονται στο έδαφος. Όταν λειτουργούν και οι δύο, στον ίδιο χρόνο t1, μεταφέρουν νερό όγκου 1m3 η καθεμιά.

Μεγαλύτερη ενέργεια προσφέρει στο νερό:

α) Η αντλία Α1,

β) Η αντλία Α2,

γ) και οι δύο αντλίες προσφέρουν την ίδια ενέργεια στο νερό.

Συνέχεια...