Κάπου προς τα τέλη της περσινής χρονιάς μελετήσαμε για πρώτη φορά τον κύκλο...... ίσως χρειάζεται ένα μικρό φρεσκάρισμα. Γι 'αυτό στο σημερινό μας μάθημα ξαναμελετήσαμε ποια είναι τα βασικά στοιχεία ενός κύκλου και πώς να σχεδιάζουμε κύκλους:
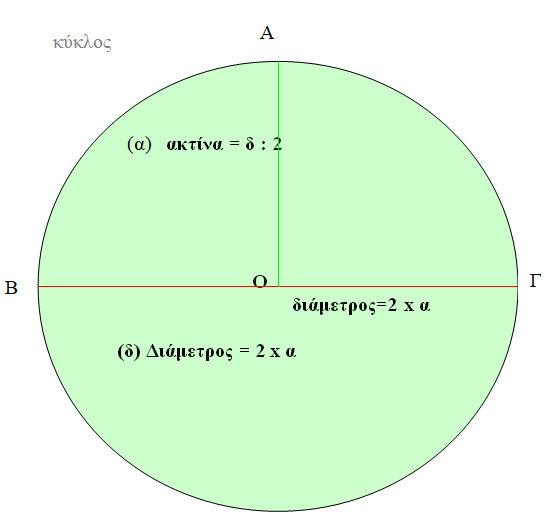
Κύκλος είναι το επίπεδο γεωμετρικό σχήμα του οποίου τα σημεία απέχουν όλα εξίσου από ένα σημείο, το κέντρο του κύκλου
Τα βασικά στοιχεία του κύκλου
Ακτίνα : Κάθε ευθύγραμμο τμήμα που αρχίζει από το κέντρο του κύκλου και καταλήγει σε κάποιο σημείο της περιφέρειάς του λέγεται ακτίνα. Όλες οι ακτίνες του ίδιου κύκλου είναι ίσες μεταξύ τους ΚΑΙ είναι άπειρες.
Διάμετρος : Είναι το ευθύγραμμο τμήμα που περνάει από το κέντρο του κύκλου και ενώνει δύο σημεία της περιφέρειας του κύκλου. Η διάμετρος ενός κύκλου είναι διπλάσια της ακτίνας και αντίστοιχα η ακτίνα είναι το μισό της διαμέτρου.
Μήκος Κύκλου: Είναι η περιφέρεια του κύκλου (αυτό που στα άλλα σχήματα το ονομάζουμε περίμετρο). Για να το υπολογίσουμε πολλαπλασιάζουμε τον αριθμό π με τη διάμετρο του κύκλου.
Μήκος κύκλου = π Χ δ = 3,14 Χ δ
Ο αριθμός που συμβολίζεται με το ελληνικό γράμμα π είναι ένας δεκαδικός αριθμός με δεκαδικά ψηφία που δεν τελειώνουν ποτέ. Στους υπολογισμούς για ευκολία χρησιμοποιούμε μόνο δύο. Έτσι π=3,14
Έγιναν: θεωρία στο τετράδιο γεωμετρίας και οι παρακάτω ασκήσεις
- Η ακτίνα α ενός κύκλου είναι 1,5 εκ. Βρίσκω τη διάμετρο του κύκλου, το μήκος του και μετά τον σχεδιάζω.
- Η διάμετρος δ ενός κύκλου είναι 5 εκ. Βρίσκω την ακτίνα του κύκλου, το μήκος του και τον σχεδιάζω.
- Ένας κύκλος έχει μήκος 20 cm περισσότερο από έναν άλλο. Πόσο μεγαλύτερη είναι η ακτίνα του;
- Οι διάμετροι δύο κύκλων διαφέρουν κατά 5 cm. Βρίσκω πόσο διαφέρουν οι ακτίνες τους.
🏡Σπίτι: Ασκήσεις στον κύκλο



 Σπίτι: στο τετράδιο μαθηματικών
Σπίτι: στο τετράδιο μαθηματικών