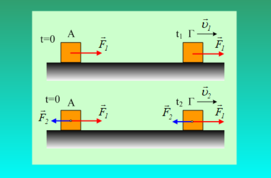
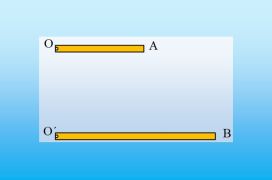
Σε λείο οριζόντιο επίπεδο ηρεμούν δυο σώματα Α και Β, με μάζες m1=1kg και m2=2kg, εμένα στα άκρα ιδανικού ελατηρίου σταθεράς k=24Ν/m. Μια σφαίρα Σ με διάμετρο ίση με το ύψος του σώματος Α και μάζα m=0,5kg κινείται
ευθύγραμμα κατά μήκος του άξονα του ελατηρίου με σταθερή ταχύτητα υ=0,9m/s και τη στιγμή t=0, συγκρούεται κεντρικά και ελαστικά με το σώμα Α, όπως στο σχήμα.
i) Να υπολογιστεί η κινητική ενέργεια του σώματος Α, αμέσως μετά την κρούση.
ii) Για το σύστημα των σωμάτων Α και Β, να βρεθούν:
α) Η μέγιστη και η ελάχιστη κινητική ενέργεια του συστήματος.
β) Οι επιταχύνσεις των δύο σωμάτων, τη στιγμή t1, όπου για πρώτη φορά παρουσιάζεται η ελάχιστη κινητική ενέργεια του συστήματος.
γ) Η μέγιστη ταχύτητα την οποία θα αποκτήσει τη στιγμή t2 για πρώτη φορά το σώμα Β. Πόση ταχύτητα θα έχει τη
στιγμή αυτή το σώμα Α;
iii) Για καθηγητές μόνο: Να βρεθούν οι παραπάνω αναφερόμενες χρονικές στιγμές t1 και t2 καθώς και η απόσταση μεταξύ της σφαίρας και του σώματος Α, τις στιγμές αυτές, αν το ελατήριο έχει φυσικό μήκος 0,6m.
ή