Category: Μαθηματικά Στ’ τάξη

Σήμερα συνεχίσαμε να κάνουμε εξάσκηση στο Εμβαδόν πλάγιο παραλληλογράμμου.

Έγιναν: ασκήσεις στο τετράδιο γεωμετρίας

🏡Σπίτι: Τ.Ε. δ τεύχος σελ. 21 ασκ.1-2-3

Σήμερα ολοκληρώσαμε τις περιπτώσεις που μπορεί κανείς να συναντήσει πρόβλημα που να λύνεται με αναγωγή στην κλασματική μονάδα.

Γ' περίπτωση: Ξέρω κάποιο μέρος και ψάχνω κάποιο άλλο μέρος

Έγιναν: ασκήσεις στο τετράδιο μαθηματικών

🏡Σπίτι: αναγωγή στην κλασματική 3

Β' περίπτωση: Ξέρω μέρος του ποσού και ψάχνω όλη την ποσότητα.

Έγιναν: στο τετράδιο μαθηματικών ασκήσεις

🏡Σπίτι: αναγωγή στην κλασματική 2

Σήμερα θυμηθήκαμε πώς μπορούμε να εφαρμόσουμε τη μέθοδο της αναγωγής της μονάδας στα κλάσματα.

Αναγωγή στην κλασματική μονάδα

Α' περίπτωση: Όταν γνωρίζουµε ολόκληρη την ποσότητα και θέλουµε να υπολογίσουµε κάποιο κλασµατικό µέρος της.

Έγιναν:  Τ.Ε. σελ. 8 προβλήματα 2, σελ. 10 πρόβλημα 2-3 και ασκήσεις στο τετράδιο μαθηματικών

🏡Σπίτι: αναγωγή στην κλασματική 1

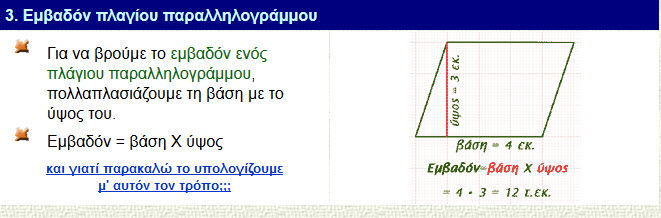
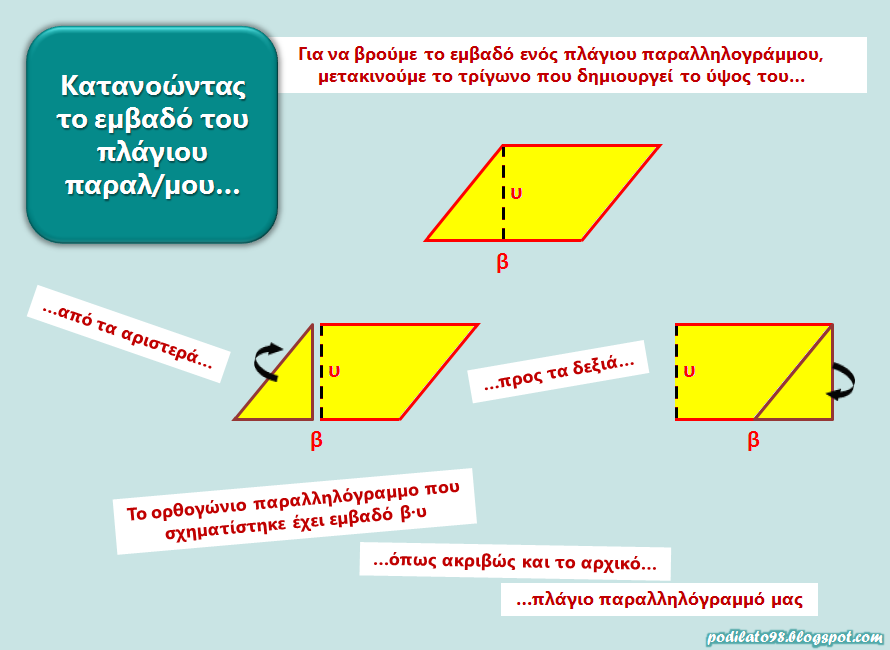
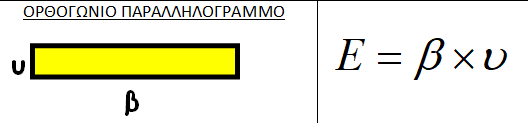
Ένα πλάγιο παραλληλόγραμμο με βάση β και ύψος υ έχει την ίδια επιφάνεια με ένα ορθογώνιο παραλληλόγραμμο που έχει την ίδια βάση β και το ίδιο ύψος υ.

Έγιναν: ασκήσεις στο τετράδιο γεωμετρίας

🏡Σπίτι: τις δύο πρώτες ασκήσεις από εμβαδόν πλάγιου ασκήσεις

"Το κλάσμα συμβολίζει την πράξη της διαίρεσης"!

• Κάθε κλάσμα είναι ίσο με το πηλίκο μιας διαίρεση: (αριθμητής) : (παρονομαστή)
• Αντίστροφα κάθε διαίρεση μπορούμε να την εκφράσουμε και ως κλάσμα.
• Κάθε κλάσμα μπορεί να εκφραστεί ως δεκαδικός αν κάνουμε τη διαίρεση.
• Αν η διαίρεση είναι ατελής σταματάμε όπου μας χρειάζεται.
• Κάθε δεκαδικός μπορεί να μετατραπεί σε κλάσμα.

Έγιναν: Βιβλίο σελ. 47

🏡Σπίτι: Τ.Ε. σελ. 9 ασκ. 1-2-3-4- πρόβλημα 1ο

Σήμερα θυμηθήκαμε τους μεικτούς αριθμούς.

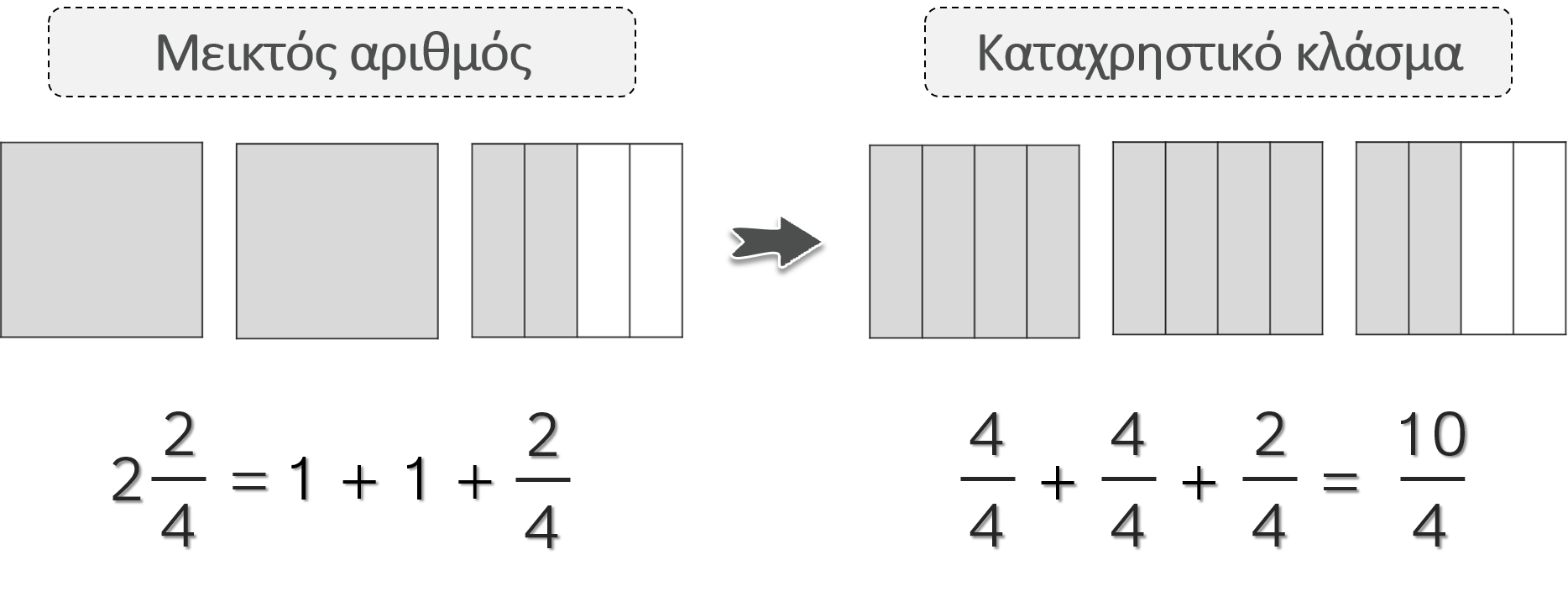
Έγιναν: Τετράδιο μαθηματικών ασκήσεις.

🏡Σπίτι: μεικτοί αριθμοί ασκήσεις

 

Σήμερα ξεκινήσαμε μια γνώριμη ενότητα από πέρσι: Τα ΚΛΑΣΜΑΤΑ!

Συγκεκριμένα σήμερα θυμηθήκαμε:

Τι είναι τα κλάσματα;

Όροι Κλάσματος

Τι εκφράζει;

Είδη κλασμάτων σε σύγκριση με τη μονάδα

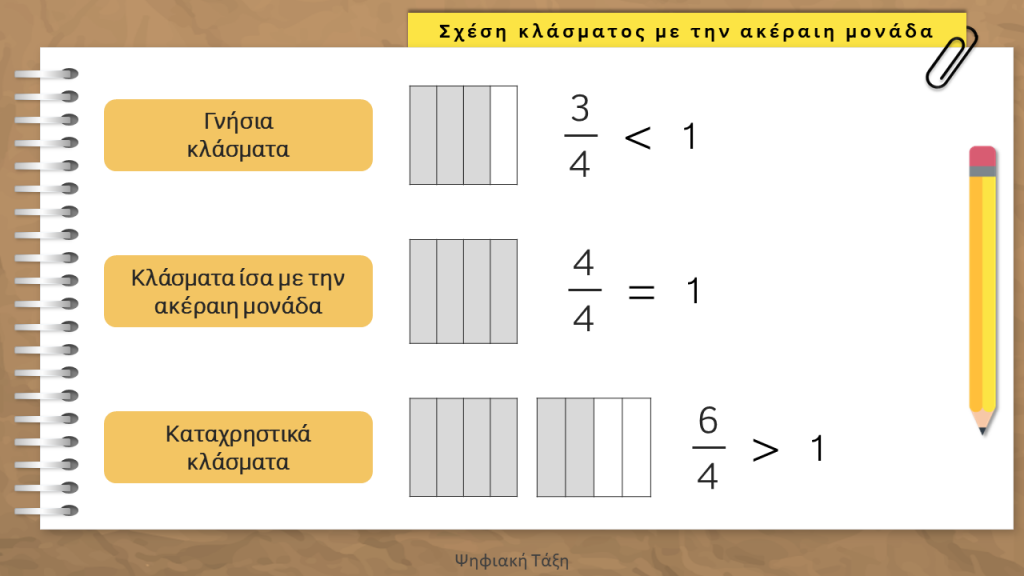
Έγιναν: Θεωρία και ασκήσεις στο τετράδιο και Βιβλίο σελ. 45

🏡Σπίτι: Τ.Ε. σελ. 7 ασκ. 1-2-3 και άσκηση μέρα 1

 

 

Σήμερα ασχοληθήκαμε με πιο σύνθετα προβλήματα και ασκήσεις σχετικά με το εμβαδόν και τις μετατροπές των μονάδων μέτρησης.

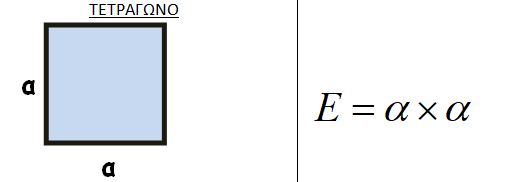
Έγιναν: Από ασκήσεις εμβαδόν και μετατροπές  έγιναν οι ασκήσεις 9-10

🏡Σπίτι: Τ.Ε. σελ. 19-20 ασκ. 1-2-πρόβλημα 1

Το σημερινό μας μάθημα ήταν αφιερωμένο στην τελική επανάληψη και σε εξάσκηση.

Έγιναν: επαναληπτικές ασκήσεις 12-18