Category: Μαθηματικά Ε’ τάξη

Μαθηματικά 19/12: Σύγκριση ετερώνυμων κλασμάτων

Σήμερα μελετήσαμε πώς μπορούμε να μετατρέψουμε τα ετερώνυμα κλάσματα σε ομώνυμα ώστε να τα συγκρίνουμε:

Έγιναν: ασκήσεις στο τετράδιο μαθηματικών

Σπίτι: Στο τετράδιο μαθηματικών μετατρέπω τα παρακάτω κλάσματα σε ομώνυμα και τα συγκρίνω:

α. 5/7-4/6       β. 9/21-2/7        γ.4/9-5/10        δ. 4/7-3/5

ε. 2/7- 3/8      στ. 8/16- 3/8       ζ. 7/9- 6/7

Μαθηματικά 16/12: Σύγκριση και Διάταξη κλασμάτων

Σήμερα αφιερώσαμε το μεγαλύτερο μέρος της ημέρας μας στα Μαθηματικά (Δεν κάναμε γλώσσα).

Αρχικά, εξηγήσαμε πάλι τα ανάγωγα κλάσματα και κάναμε εξ΄άσκηση στο τετράδιό μας.

Στη συνέχεια ήρθε η ώρα για σύγκριση. Συγκεκριμένα μελετήσαμε δύο περιπτώσεις: Πώς συγκρίνουμε ομώνυμα κλάσματα και πώς συγκρίνουμε κλάσματα με ίδιο αριθμητή αλλά διαφορετικό παρονομαστή.

Έγιναν: Βιβλίο σελ. 47, θεωρία στο τετράδιο μαθηματικών και οι ασκήσεις της φωτοτυπίας: Σύγκριση- Διάταξη Κλασμάτων

Σπίτι: Τ.Ε. σελ. 45 ασκ. 3, σελ. 47 ασκ.1,3 και σελ. 48 ασκ.6

Μαθηματικά 12/12: Πώς φτιάχνω ισοδύναμα κλάσματα

Στο σημερινό μας μάθημα συνεχίσαμε να μελετάμε τα ισοδύναμα κλάσματα και συγκεκριμένα είδαμε με ποιους τρόπους μπορούμε να φτιάξουμε ισοδύναμα:

Έγιναν: Ασκήσεις στο τετράδιο μαθηματικών

Επίσης, μελετήσαμε τα ανάγωγα κλάσματα!

Ο λόγος για τον οποίο ένα κλάσμα που δεν απλοποιείται ονομάστηκε ανάγωγο είναι προφανής αφού ανάγωγο λέμε κάποιον που δεν συμπεριφέρεται καλά. Κι ένα κλάσμα που δεν απλοποιείται, δεν συμπεριφέρεται καλά ή τουλάχιστον δεν συμπεριφέρεται όπως εμείς θα θέλαμε.
Παραδείγματα ανάγωγων κλασμάτων είναι τα: \frac{3}4 , \frac{8}5 κ.α.
Για να φτιάξω ένα ανάγωγο κλάσμα αρκεί να διαιρέσω τον αριθμητή και τον παρονομαστή με τον ΜΚΔ τους.
Έγιναν: Ασκήσεις στο τετράδιο μαθηματικών και Τ.Ε. σελ. 45 ασκ.3

🏡Σπίτι: ασκήσεις στο τετράδιο μαθηματικών:

  • Βρίσκω τρία ισοδύναμα κλάσματα με μεγαλύτερους όρους: 4/6, 2/8
  • Βρίσκω τρία ισοδύναμα κλάσματα με μικρότερους όρους: 20/40, 32/48

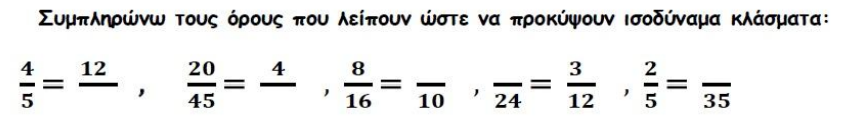
Μαθηματικά 9/12: Ισοδύναμα κλάσματα- Τι είναι; Πώς ελέγχουμε αν είναι ισοδύναμα;

Νέο μάθημα σήμερα και μελετήσαμε μια καινούρια (ή και όχι τόσο καινούρια) κατηγορία κλασμάτων:

Ισοδύναμα κλάσματα

Δύο ή περισσότερα κλάσματα που έχουν διαφορετικούς όρους, δηλαδή διαφορετικό αριθμητή & παρονομαστή, αλλά εκφράζουν την ίδια ποσότητα, λέγονται ισοδύναμα.

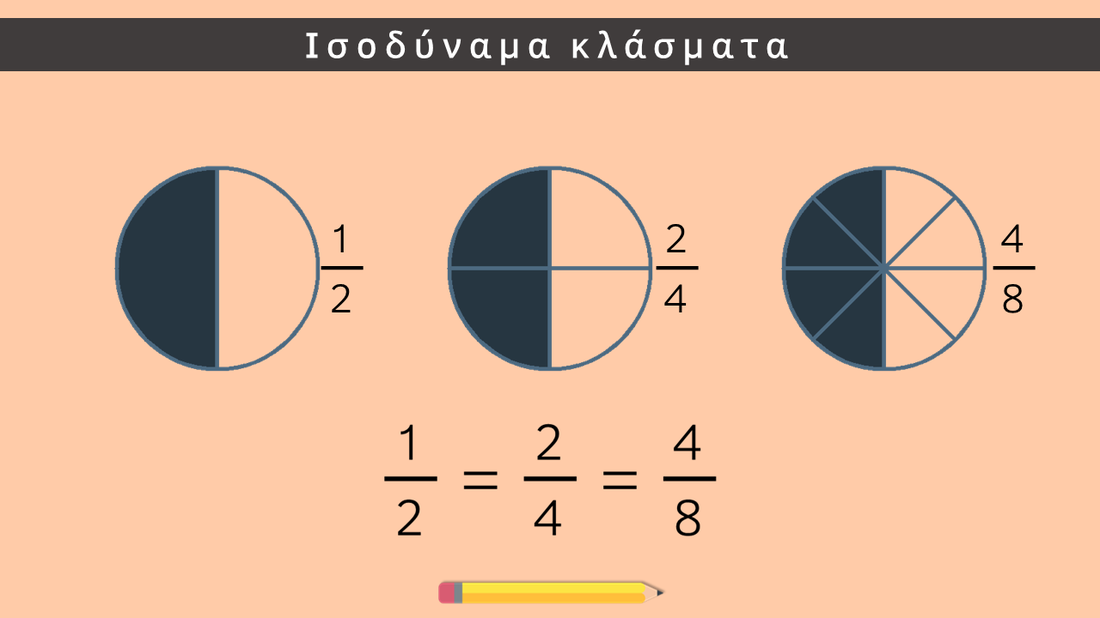
Πώς ελέγχω αν δύο κλάσματα είναι ισοδύναμα;

Κάνω "χιαστί γινόμενα": Πολλαπλασιάζω τον αριθμητή του ενός με τον παρονομαστή του άλλου. Αν τα δύο γινόμενα είναι ίσα, τότε τα κλάσματα είναι ισοδύναμα!

Έγιναν: Βιβλίο σελ. 45 ασκ.1, Τ.Ε. ασκ. 1 σελ. 45 και ασκήσεις στο τετράδιο μαθηματικών.

Σπίτι΅: ασκήσεις φωτοτυπίας

 

Μαθηματικά 8/12: Επανάληψη στους μεικτούς αριθμούς

Σήμερα κάναμε ένα "έκτακτο" μάθημα Μαθηματικών για να κάνουμε μια μικρή επανάληψη στους μεικτούς αριθμούς.

Έγιναν οι ασκήσεις της παρακάτω φωτοτυπίας: επαναληπτικές 13-15

Στο σπίτι ολοκληρώνουμε τις ασκήσεις της φωτοτυπίας.

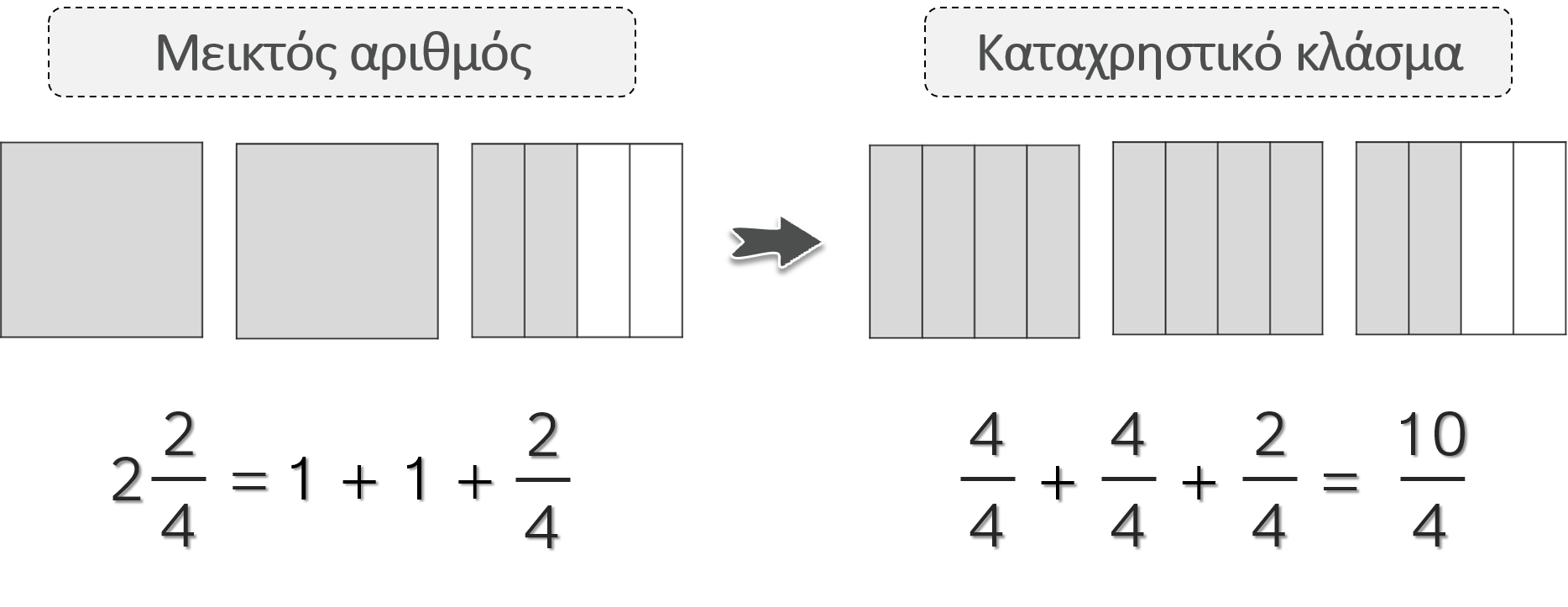
Μαθηματικά 7/12: Πώς μετατρέπω το μεικτό αριθμό σε καταχρηστικό κλάσμα

Σήμερα είδαμε την αντίστροφη διαδικασία:

🏡Σπίτι

Τετράδιο μαθηματικών: μετατρέπω τους μεικτούς αριθμούς σε καταχρηστικά κλάσματα

Μαθηματικά 6/12: Μετατροπή καταχρηστικού κλάσματος σε μεικτό αριθμό

Στο σημερινό μάθημα μελετήσαμε πώς μπορούμε να μετατρέψουμε ένα καταχρηστικό κλάσμα σε μεικτό αριθμό.

Σπίτι: Τ.Ε. σελ. 43 ασκ.2

Τετράδιο μαθηματικών: μετατρέπω τα καταχρηστικά κλάσματα σε μεικτούς αριθμούς με τον τρόπο της διαίρεσης: 35/4, 78/9, 146/3, 57/10, 159/13, 28/11

Μαθηματικά 5/12: Μεικτοί Αριθμοί

Σήμερα ξεκινήσαμε να μελετάμε τους Μεικτούς Αριθμούς!

  • Μεικτός ονομάζεται ο αριθμός που αποτελείται από ακέραιο μέρος και κλασματικό μέρος.
  • Ένας μεικτός αριθμός μπορεί να μετατραπεί σε καταχρηστικό κλάσμα και το αντίστροφο.

🏡Σπίτι: Τ.Ε. σελ. 41 ασκ.1

Τετράδιο μαθηματικών:

  1. Μετατρέπω τα παρακάτω κλάσματα σε μεικτούς αριθμούς, αναλύοντάς τα: 18/4, 36/8, 25/4, 72/13, 29/2, 44/5, 128/30