Είδαμε στην Εισαγωγή μαθηματικών παραστάσεων και συμβόλων σε άρθρα και σελίδες πως μπορούμε να εισάγουμε μαθηματικά σύμβολα και παραστάσεις σε ένα άρθρο ή σε μια σελίδα.
Εδώ θα δούμε πως μπορούμε να εισάγουμε πιο προηγμένα στοιχεία. Προσέξτε πως σε κάποιες περιπτώσεις δεν χρησιμοποιούμε τα διπλά δολάρια ή τις τετράγωνες αγκύλες. Η εισαγωγή ξεκινάει με την (ανάποδη) πλάγια γραμμή (\). Και φυσικά στην αρχή του άρθρου ή της σελίδας μας πρέπει να υπάρχει η οδηγία [latexpage]
Παραδείγματα
| Στοιχείο | Γράφουμε | Εμφανίζεται |
Στοίχιση (στον χαρακτήρα που ακολουθεί το &)
Ο αστερίσκος ( |
\begin{align*} |
|
| Αρίθμηση σχέσεων | \begin{equation} \label{eq:poly} |
(1) |
| Αναφορά σε σχέση | Όπως στη σχέση (\ref{eq:poly}) |
Όπως στη σχέση (1) |
Πίνακες, ορίζουσες (χρησιμοποιούμε $$ $$)
Αν δεν θέλουμε στοίχιση παραλείπουμε τα |
$$\begin{matrix}a & bbb & ccccc \\ ddd & ee & f \end{matrix}$$
|
|
Περιπτώσεις (χρησιμοποιούμε $$ $$) |
$$ multicase \begin{cases} |
|
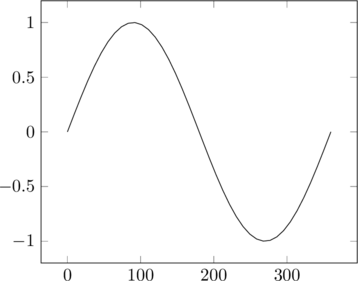
| Σχεδίαση γραφικών παραστάσεων 2 διαστάσεων (γωνίες σε μοίρες)
ημ(x) |
\begin{tikzpicture} |
|
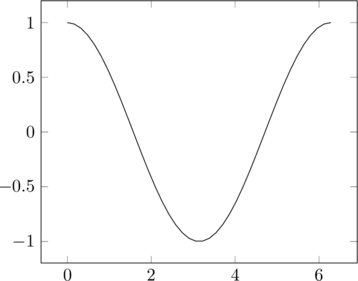
| Σχεδίαση γραφικών παραστάσεων 2 διαστάσεων (γωνίες σε ακτίνια)
συν(x) |
\begin{tikzpicture} |
|
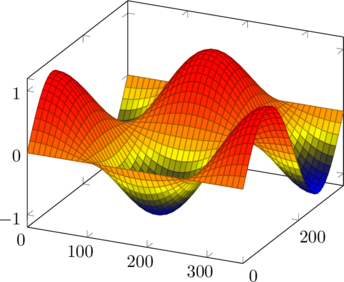
| Σχεδίαση γραφικών παραστάσεων 3 διαστάσεων (γωνίες σε μοίρες)
συν(x) ημ(y) |
\begin{tikzpicture} |
|
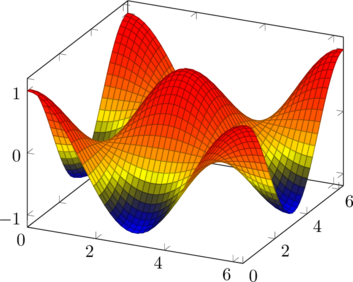
| Σχεδίαση γραφικών παραστάσεων 3 διαστάσεων (γωνίες σε ακτίνια)
συν(x) συν(y) |
\begin{tikzpicture} |
|
ΠΡΟΣΟΧΗ: Η ύπαρξη πολλών γραφικών, ιδίως τριών διαστάσεων "βαραίνει" πολύ την εμφάνιση.
Η σελίδα θα εμπλουτίζεται διαρκώς.


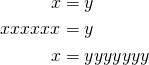
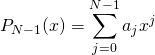
![Rendered by QuickLaTeX.com \[\begin{vmatrix} a_{1,1} & a_{1,2} & \cdots &a_{1,n}\\a_{2,1} & a_{2,2} & \cdots &a_{2,n}\\ \vdots & \vdots & \ddots & \vdots \\ a_{n,1} & a_{n,2} & \cdots &a_{n,n}\end{vmatrix}\]](https://blogs.e-me.edu.gr/nskoulid/wp-content/ql-cache/quicklatex.com-b3f074386a63ccfe7f3b6680a58fb9cb_l3.png)
![Rendered by QuickLaTeX.com \[\alpha \chi +\beta =0 \begin{cases}\alpha \ne 0 & \chi =-\frac {\beta } {\alpha }\\ \alpha =0, \beta \ne 0 & \textup{αδύνατη} \\ \alpha =0, \beta =0 & \textup{αόριστη }\\ \end{cases}\]](https://blogs.e-me.edu.gr/nskoulid/wp-content/ql-cache/quicklatex.com-97128debe5d3efebc296718f73f628c4_l3.png)
Πρόσφατα Σχόλια